Website owner:  James Miller

Products, quotients and roots of complex numbers in polar form. De Moivre’s theorem. Roots of unity

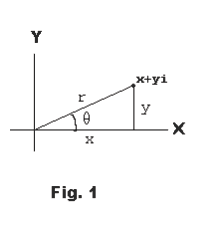
Polar representation of a complex number. The polar representation of the complex number

                        z = x + iy

is                                                                                  

            z = x + iy = r (cos θ + i sin θ)

where

                      x = r cos θ

                      y = r sin θ

                     θ = arctan (y/x)

See Figure 1. The radius vector r is called the modulus or absolute value of the complex number and the polar angle θ is called the amplitude or argument of the number. The argument θ of a complex number z is often denoted by arg z. The abbreviation cis θ is sometimes used for cos θ + i sin θ. In polar coordinates a point P is often specified by the number pair (r, θ).

Product of two complex numbers in polar form. The product z₁z₂ of the two complex numbers

                        z₁ = r₁ (cos θ₁ + i sin θ₁)

and

                        z₂ = r₂ (cos θ₂ + i sin θ₂)

is

1)                    z₁z₂ = r₁r₂[cos (θ₁ + θ₂) + i sin (θ₁ + θ₂)] ,

a result which can be easily obtained by utilizing the trigonometric identities

            sin(A B) = sin A cos B cos A sin B

            cos(A B) = cos A cos B sin A sin B .

Quotient of two complex numbers in polar form. The quotient z₁/z₂ of the two complex numbers

                        z₁ = r₁ (cos θ₁ + i sin θ₁)

and

                        z₂ = r₂ (cos θ₂ + i sin θ₂)

is

2)         z₁/z₂ = ( r₁/r₂) [cos (θ₁ - θ₂) + i sin (θ₁ - θ₂)]

De Moivre’s Theorem. For any complex number z = r( cos θ + i sin θ )

3)        zⁿ = [ r(cos θ + i sin θ)]ⁿ = rⁿ (cos nθ + i sin n)

This formula holds for every real value of the exponent n. For example, if the exponent is a fraction 1/n, we get

Rules of arguments. If

            z₁ = r₁ (cos θ₁ + i sin θ₁)

            z₂ = r₂ (cos θ₂ + i sin θ₂)

            w = z^a

where a is a real number, then by 1), 2) and 3 ) above

1]        arg (z₁z₂) = arg z₁ + arg z₂

2]        arg (z₁/z₂) = arg z₁ - arg z₂

3]        arg w = a arg z

Def. N-th root of a number. Let n be a positive integer. If aⁿ = b, then a is said to be the n-th root of b.

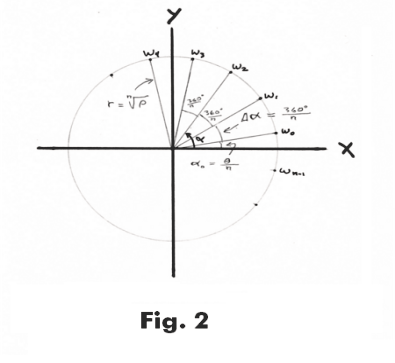
Roots of complex numbers in polar form. The n distinct n-th roots of the complex number

           z = r( cos θ + i sin θ)

can be found by substituting successively k = 0, 1, 2, ... , (n-1) in the formula

Derivation

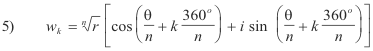
The n roots are equally spaced around the circumference of a circle in the complex plane. See Figure 2. If the complex number for which we are computing the n n-th roots is z = ρ( cos θ + i sin θ) the radius of the circle will be

and the first root w₀ corresponding to k = 0 will be at an amplitude of α = θ/n. This root will be followed by the n-1 remaining roots at equal distances apart. The angular amplitude between each root is Δα = 360^o/n.

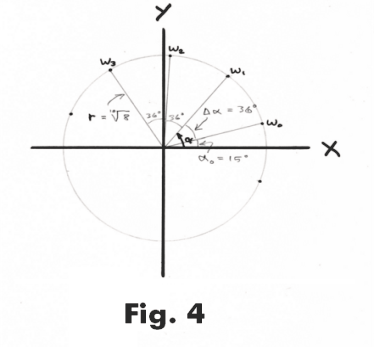
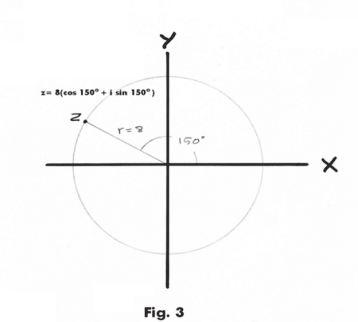
Example. Suppose we wish to compute the ten 10-th roots of z = 8(cos 150^o + i sin 150^o) shown in Fig. 3. The ten roots w₀, w₁, .... , w₉ would be spaced evenly around a circle as shown in Fig. 4. The first root, w₀, would be at an amplitude of α = 150/10 = 15^o. The rest of the roots would be spaced at Δα = 360/10 = 36^o intervals.

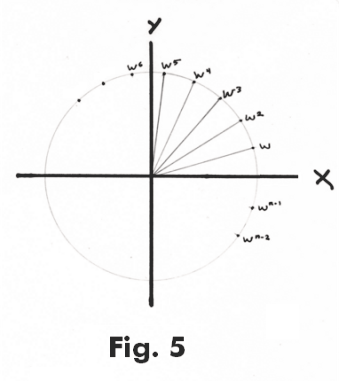
Roots of unity. The n n-th roots of 1 are obtained from 5) above by letting r = 1 and θ = 0. They are

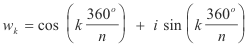
for k = 0, 1, 2, ... , (n-1)

Let us denote the root corresponding to k = 1 by w. This root w is then given by

The n n-th roots of 1 then correspond to powers of w:

        w, w², w³, ... ,wⁿ

 where wⁿ = 1

The roots are equally spaced around the circumference of a unit circle in the complex plane. See Figure 5.

Primitive roots of unity. Of the n n-th roots of 1 some of the roots may be m-th roots of 1 where m is some integer less than n. For example, the 6 sixth roots of 1 are

            r₁ = w

            r₂ = w²

            r₃ = w³

            r₄ = w⁴

            r₅ = w⁵

            r₆ = w⁶ = 1

Of these, r₃ = w³ and r₆ = w⁶ are square roots of 1 and r₂ = w², r₄ = w⁴ and r₆ = w⁶ are cube roots of 1. The primitive roots of 1 are those roots which are not m-th roots of 1 for some 0 < m < n. Thus in the example just given the roots r₁ = w and r₅ = w⁵ are primitive roots of 1. In other words, of the n n-th roots of 1, a particular n-th root r is a primitive root if and only if r^m 1 for any integer m less than n.

Theorem Let w, w², w³, ... ,wⁿ be the n n-th roots of 1. Let m be any integer 0 < m < n and let d be the greatest common divisor (m,n) of m and n. If d > 1 then , w^m is an n/d-th root of 1.

 Example. Let m = 3 and n = 6. Then d = (m,n) = (3,6) = 3 and n/d = 2. Thus w³ is a square root of 1.

Corollary. The primitive n-th roots of 1 are those and only those n-th roots w, w², w³, ... ,wⁿ of 1 whose exponents are relatively prime to n.

Roots of a complex number in terms of the roots of unity. Let

                 z = a + bi = r( cos θ + i sin θ )

and

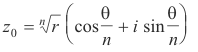
Then the n n-th roots of z are

            z₀, wz₀, w²z₀, ... ,w ^k-1z₀

where  

References.

  James & James. Mathematics Dictionary.

  Brink. A First Year of College Mathematics.

  Spiegel. College Algebra.

  Hauser. Complex Variables with Physical Applications.