Curve fitting. The method of least squares.

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

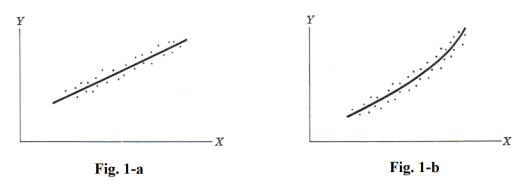
In science and engineering we are always making measurements and, for various reasons, measurements invariably contain some error. For example Fig. 1 shows the plots obtained from measurements of two different phenomena. In Fig 1-a the plotted points obviously follow a straight line. In Fig. 1-b they obviously follow a curve. Such plots of measurements are often called scatter diagrams. Exactly where does the true line or curve actually lie? How do we determine it? Well, one way is to establish the curve is to look at the scatter diagram and simply draw in the line or curve where we think it should be. But there is another way. It is done by what is called “the Method of Least Squares”. Points from measurements may follow a straight line or they follow some curve such as a parabola, hyperbola, or some other curve. To use the Method of Least Squares we must first hypothesize as to what curve they follow.

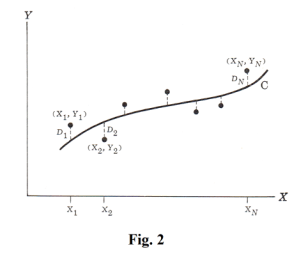
To motivate a possible technique for finding a best line or curve consider Fig. 2. Here a curve C has been postulated. For each of the discrete values x₁, x₂, ... , x_N of x there is a vertical distance shown in the figure as D₁, D₂, ... , D_N between the corresponding point and the curve. This distance D_i is sometimes referred to as the deviation, error or residual and may be positive, negative or zero.

A measure of the “goodness of fit” of the curve C to the given data is provided by the quantity

If this is small the fit is good. If it is large, the fit is bad. We thus make the following definition

Definition. Of all curves approximating a given set of points, the curve having the property that

is called a best fitting curve.

A curve having this property is said to fit the data in the least square sense and is called a least square curve. A line having this property is called a least square line, a parabola having this property is called a least square parabola, etc.

It is customary to employ the above definition when x is the independent variable and y is the dependent variable. If y is the independent variable and x is the dependent variable we use horizontal deviations instead of vertical deviations — which will lead to different least square curves.

The least square line. The least square line approximating the set of points (x₁, y₁), (x₂, y₂), .... , (x_n, y_n) is given by the equation

1) y = a₀ + a₁x

where the constants a₀ and a₁ are determined by solving simultaneously the system of equations

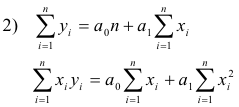
for a₀ and a₁. Proof. These equations, called the normal equations for the least square line, are easily remembered by observing that the first equation is obtained formally by summing on both sides of 1) i.e. Σy = Σ(a₀ + a₁x) and the second equation is obtained formally by first multiplying both sides of 1) by x and then summing i.e. Σxy = Σx(a₀ + a₁x) = a₀Σx + a₁Σx².

Solution of the normal equations gives the following values for a₀ and a₁:

If the variable x is taken as the dependent instead of the independent variable we write 2) as x = b₀ + b₁y. Then the above results hold if x and y are interchanged and a₀and a₁ are replaced by b₀ and b₁ respectively. The resulting least square line, however, will not be the same as the one obtained above.

The least square parabola. The least square parabola approximating the set of points (x₁, y₁), (x₂, y₂), .... , (x_n, y_n) is given by the equation

4) y = a₀ + a₁x + a₂x²

where the constants a₀, a₁ and a₂ are determined by solving simultaneously the system of equations

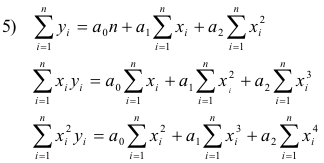
for a₀, a₁ and a₂ . These equations, called the normal equations for the least square parabola, are easily remembered by observing that they can be obtained formally by multiplying equation 4) by 1, x, and x₂ respectively and summing on both sides of the resulting equations. This technique can be extended to obtain normal equations for least square cubic curves, least square quartic curves and in general least square curves of type

y = a₀ + a₁x + a₂x² + ..... + a_nxⁿ.

Problems involving more than two variables. Problems involving more than two variables can be treated in a manner analogous to that for two variables. For example, there may be a relationship between the three variables x, y, and z which can be described by the equation

6) z = a₀ + a₁x + a₂y

which is called a linear equation in the variables x, y and z.

In a three dimensional rectangular coordinate system this equation represents a plane. The sample points (x₁, y₁, z₁), (x₂, y₂, z₂), .... , (x_n, y_n, z_n) may be scattered in space in such a way as to suggest they approach some “approximating plane”. By extension of the method of least squares, we can speak of a least square plane approximating the data. The normal equations corresponding to the least square plane 6) are given by

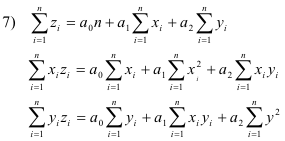
and can be remembered as obtained from 6) by multiplying by 1, x, and y successively and then summing.

References

Murray R Spiegel. Statistics (Schaum Publishing Co.)