Student’s t distribution. The chi-square distribution. Confidence intervals. Tests of hypotheses and significance.

SolitaryRoad.com

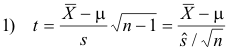
Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

Small sampling theory. Student’s t distribution. The chi-square distribution. Confidence intervals. Tests of hypotheses and significance.

Small sampling theory. A study of sampling distributions of statistics employing small samples is called small sampling theory. A more suitable name, however, would be exact sampling theory since the results obtained hold for large as well as small samples. By a small sample we mean a sample of size n < 30.

Two important distributions used for the case of small samples is the Student’s t distribution and the chi-square distribution.

Student’s t distribution. Let us first define the statistic

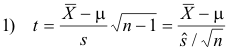
which is analogous to the statistic given by

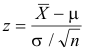
Here:

s — sample standard deviation

n — sample size

μ and σ — population mean and standard deviation

is the modified standard deviation where

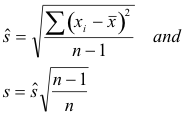
If we consider samples of size n drawn from a normal (or approximately normal) population with mean μ and if for each sample we compute t, using the sample mean and the sample standard deviation s or , the sampling distribution for t can be obtained. This distribution (see Fig. 1), called the Students’s t distribution, is given by

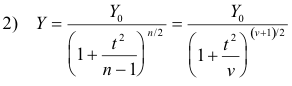
where Y₀ is a constant depending on n such that the total area under the curve is one and the constant ν = n -1 is called the number of degrees of freedom. (The definition of degrees of freedom will be given later.)

Let us now go over the above computational process step by step in more detail.

1. We take m samples, each of sample size n

2. On each sample we compute the sample mean , the sample standard deviation s, and the value of t from the formula

using the sample mean as an approximation for the population mean μ.

For large m the values of t will follow Student’s t distribution 2).

This distribution is named after its discoverer Gosset, who published his works under the pseudonym “Student” during the early part of the twentieth century.

For large values of ν or n (certainly n > 30) the curves closely approximate the standardized normal curve

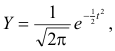
as shown in Fig. 1.

Percentile. A value on a scale of 100 that indicates the percent of a distribution that is equal to or below it. It is a way of expressing where an observation falls in a range of other observations. For example, if a score falls in the 20th percentile, this means that 20 percent of all the scores recorded are lower.

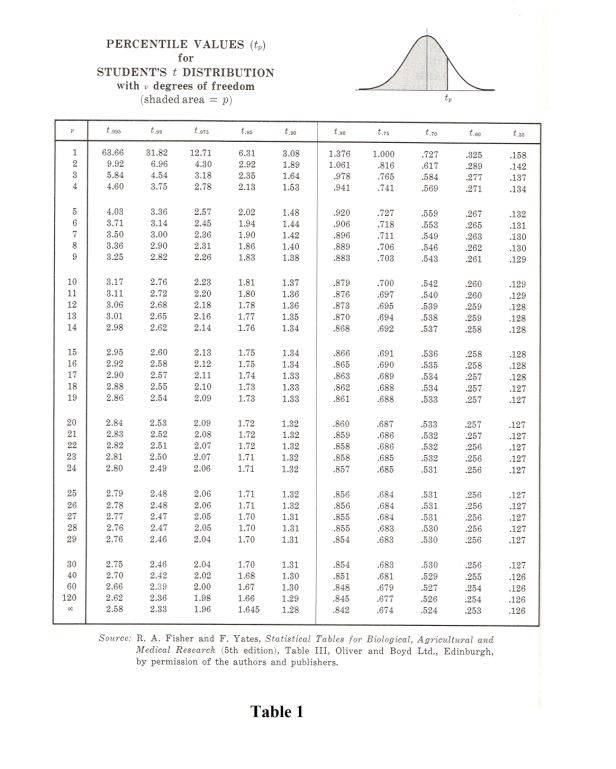
Confidence intervals. We can define 95%, 99% or other confidence intervals by using the table of the t distribution. See Table 1.

For example, if -t.₉₇₅ and t.₉₇₅ are the values of t for which 2.5% of the area lies in each “tail” of the t distribution, then a 95% confidence interval for t is

With some algebraic manipulation we obtain

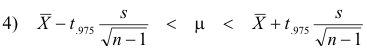
from which we see that μ is estimated to lie in the interval given by 4) with 95% confidence (i.e. probability .95). Note that t.₉₇₅ represents the 97.5 percentile value, while -t.₉₇₅ = -t.₉₇₅ represents the 2.5 percentile value.

In general, we can represent confidence limits for population means by

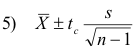
where the values +t_c, called critical values or confidence limits, depend on the level of confidence

desired and the sample size. They can be read from Table 1.

Tests of hypotheses and significance. The tests of hypotheses and significance used for large samples are easily extended to problems involving small samples, the only difference being that the z score or z statistic is replaced by a suitable t score or t statistic.

1. Means

To test the hypothesis H₀ that a normal population has mean μ, we use the t score or t statistic

where is the mean of a sample of size n.

This is analogous to using the z score,

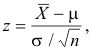
for large n except that

is used in place of σ. The difference is that while z is normally distributed, t follows Student’s distribution. As n increase, these tend toward agreement.

2. Differences of Means

Suppose that two random samples of sizes n₁ and n₂ are drawn from normal populations whose standard deviations are equal (σ₁ = σ₂). Suppose further that these two populations have means and standard deviations given by respectively. To test the hypothesis H₀ that the samples come from the same population (i.e. μ₁ = μ₂, as well as σ₁ = σ₂) we use the t score given by

The distribution of t is Student’s distribution with ν = n₁ + n₂ - 2 degrees of freedom.

The chi-square distribution.

Here:

s — sample standard deviation

n — sample size

μ and σ — population mean and standard deviation

Let us define the statistic

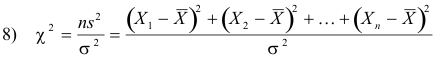
where χ is the Greek letter chi and is read chi-square.

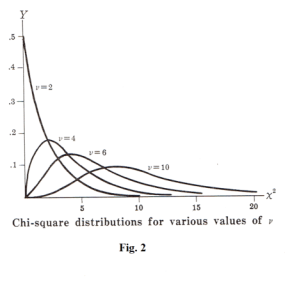
If we consider samples of size n drawn from a normal population with a standard deviation σ, and if for each sample we compute χ² , a sampling distribution for χ² can be obtained. This distribution, called the chi-square distribution, is given by

where ν = n - 1 is the number of degrees of freedom, and Y₀ is a constant depending on ν such that the total area under the curve is one. The chi-square distributions corresponding to various values of ν are shown in Fig. 2.

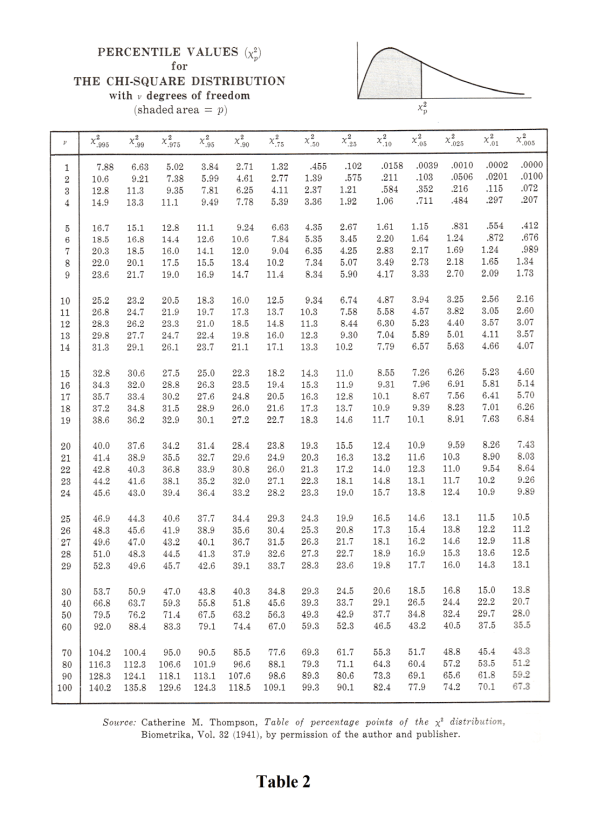
Confidence intervals for χ². As is done with the normal and t distributions, we can define 95%, 99% or other confidence limits and intervals for χ² by use of the table of the χ² distribution. See Table. 2. In this manner we can estimate within specified limits of confidence the population standard deviation σ in terms of the a sample standard deviation s.

For example, if and are the values of χ² (called critical values) for which 2.5% of the area in each “tail” of the distribution, then the 95% confidence interval is

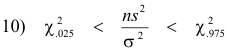
With some algebraic manipulation we obtain

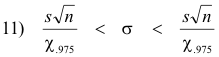
Thus σ is estimated to lie in the interval indicated with 95% confidence. Similarly other confidence intervals can be found. The values and represent respectively the 2.5 and 97.5 percentile values.

Table 2 gives percentile values corresponding to the number of degrees of freedom ν.

Degrees of freedom. In order to compute a statistic such as 1) or 8), it is necessary to use observations obtained from a sample as well as certain other parameters. If these parameters are unknown they must be estimated from a sample.

The number of degrees of freedom of a statistic generally denoted by ν is defined as the number n of independent observations in the sample (i.e. the sample size) minus the number k of population parameters which must be estimated from sample observations. In symbols, ν = n - k.

In the case of the statistic 1) the number of independent observations in the sample is n, from which we can compute and s. However, since we must estimate ν, k = 1 and so ν = n - 1.

In the case of the statistic 8) the number of independent observations in the sample is n, from which we can compute and s. However, since we must estimate σ, k = 1 and so ν = n - 1.

Portions, examples, solved problems excerpted from Murray R. Spiegel. Statistics. Schaum.

References

Murray R Spiegel. Statistics (Schaum Publishing Co.)