Elementary sampling theory. Sampling distribution of a statistic. Sampling distribution of means, standard deviations, proportions, differences and sums. Standard errors.

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

Sampling theory. Sampling theory is a study of relationships existing between a population and samples drawn from that population. It is useful, for example, in the estimation of unknown population quantities (such as population mean, variance, etc.) often called population parameters or briefly parameters, from a knowledge of corresponding sample quantities (such as sample mean, variance, etc.), often called sample statistics or briefly statistics.

Sampling theory is also useful in determining whether observed differences between two samples are actually due to chance variation or whether they are really significant. Such questions arise, for example, in testing a new serum for use in treatment of a disease or in deciding whether one production process is better than another. Answering these kinds of questions involve use of so-called tests of significance and hypotheses which are important in the theory of decisions.

Statistical inference. A study of inferences made concerning a population by use of samples drawn from it, together with indications of the accuracy of such inferences using probability theory, is called statistical inference.

In order that conclusions of sampling theory and statistical inference be valid, samples must be chosen so as to be representative of a population. A study of methods of sampling and the related problems which arise is called the design of the experiment.

One way in which a representative sample may be obtained is by a process called random sampling. In random sampling each member of a population has an equal chance of being included in the sample. One technique for obtaining a random sample is to assign numbers to each member of a population, write these numbers on small pieces of paper, place them in an urn and then draw numbers from the urn, being careful to mix thoroughly before each drawing.

Sampling with and without replacement. If we draw a number from an urn, we have the choice of replacing or not replacing the number into the urn before a second drawing. In the first case the number can come up again and again, whereas in the second it can come up only once. Sampling where each member of a population may be chosen more than once is called sampling with replacement, while if each member cannot be chosen more than once is called sampling without replacement.

Sampling distributions

Def. Sampling distribution of a statistic. Consider all possible samples of size n that can be drawn from a given population (either with or without replacement). For each sample we can compute a statistic, such as the mean, standard deviation, etc. We thus obtain a distribution of the statistic which is called its sampling distribution.

Example. Consider a normal population with a mean μ and variance σ². Assume we repeatedly take samples of a given size from this population and calculate the arithmetic mean for each sample — this statistic is called the sample mean. The distribution of these means is called the “sampling distribution of the sample mean”.

Standard error. The standard deviation of the sampling distribution of a statistic is referred to as the standard error of that quantity.

Thus the sampling distribution of a statistic is the distribution of the statistic for all possible samples of a given sample size from the given population. If, for example the particular statistic used is the sample mean, the distribution is called the sampling distribution of the means or the sampling distribution of the mean. Similarly we could have sampling distributions of standard deviations, variances, medians, proportions, etc.

For each sampling distribution, we can compute the mean, standard deviation, etc. Thus we can speak of the mean and standard deviation of the sampling distribution of means, etc.

See Fig. 1 for an example of a computation of a sampling distribution of means.

Sampling distribution of means

Theorem 1. Suppose all possible samples of size n_s are drawn without replacement from a finite population of size n_p where n_p > n_s. Let us denote the mean and standard deviation of the sampling distribution of the mean by and and the population mean and standard deviation by μ_p and σ_p respectively. Then

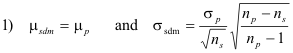
If the population is infinite or if sampling is with replacement, the above results reduce to

For sample sizes of n ≥30 the sample mean μ_s is a very close approximation to the population mean μ_p and the sample standard deviation σ_s is a very close approximation to the population standard deviation σ_p. In solving problems the population mean μ_p and standard deviation σ_p will generally not be known and the computed values of the sample mean μ_s and standard deviation σ_s are used.

For large values of n (n ≥30) the sampling distribution of means is approximately a normal distribution with mean and standard deviation irrespective of the population (so long as the population mean and variance are finite and the population size is at least the sample size).

In case the population is normally distributed, the sampling distribution of means is also normally distributed even for small values of n (i.e. n < 30).

Sampling distribution of proportions

Theorem 2. Suppose that a population is infinite and that the probability of occurrence of an event (called its success) is p while the probability of non-occurrence of the event is q = 1 - p. For example, the population may be all possible tosses of a fair coin in which the probability of the event “heads” is p = ½.

Consider all possible samples of size n_s drawn from this population, and for each sample determine the proportion P of successes. In case of the coin, P would be the proportion of heads turning up in n tosses. Then we obtain a sampling distribution of proportions whose mean and standard deviation are given by

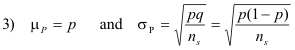
which can be obtained from 2) by placing μ = p and .

For large values of n_s (n_s ≥30) the sampling distribution is very closely normally distributed. Note that the population is binomially distributed.

The equations 3) are also valid for a finite population in which sampling is with replacement.

For finite populations in which sampling is without replacement, equations 3) are replaced by equations 1) with μ = p and .

Note that equations 3) are obtained most easily by dividing the mean and standard deviation (np and ) of the binomial distribution by n_s.

Sampling distribution of differences and sums

Theorem 3. Suppose that we are given two populations. For each sample of size n₁ drawn from the first population let us compute a statistic S₁. This yields a sampling distribution for the statistic S₁ whose mean and standard deviation we denote by and respectively. Similarly, for each sample of size n₂ drawn from the second population let us compute a statistic S₂. This yields a sampling distribution for the statistic S₂ whose mean and standard deviation are denoted by and . From all possible combinations of these samples from the two populations we can obtain a distribution of the differences, S₁ - S₂, which is called the sampling distribution of differences of the statistics. The mean and standard deviation of this sampling distribution, denoted respectively by and , are given by

provided that the samples chosen do not in any way depend on each other, i.e. the samples are independent.

If S₁ and S₂ are sample means from the two populations, which we denote by and , then the sampling distribution of the differences of means is given for infinite populations with mean and standard deviations μ₁, σ₁ and μ₂, σ₂ respectively by

and

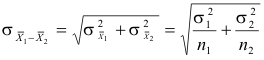
using equations 2). The result also holds for finite populations if sampling is with replacement. Similar results can be obtained for finite populations in which sampling is without replacement by using equations 1).

Corresponding results can be obtained for the sampling distributions of differences of proportions from two binomially distributed populations with parameters p₁, q₁ and p₂, q₂ respectively. In this case S₁ and S₂ correspond to the proportion of successes, P₁ and P₂, respectively. In this case S₁ and S₂ correspond to the proportion of successes, P₁ and P₂, and equations 4) yield the results

and

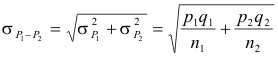
If n₁ and n₂ are large (n₁, n₂ ≥30) the sampling distributions of differences of means or proportions are very closely normally distributed.

It is sometimes useful to speak of a sampling distribution of the sum of statistics. The mean and standard deviation of this distribution are given by

Standard errors. The standard deviation of a sampling distribution of a statistic is often called its standard error. In Table 1 are listed standard errors of sampling distributions for various statistics under the conditions of random sampling from an infinite (or very large) population or sampling with replacement from a finite population. Also listed are special remarks giving conditions under which results are valid and other pertinent statements.

The sample size is denoted by N. The quantities μ, σ, p, μ_r and ,s, P, m_r denote respectively the population and sample means, standard deviations, proportions and rth moments about the mean.

It is noted that if the sample size N is large enough, the sampling distributions are normal or nearly normal. For this reason the methods are known as large sampling methods. When N < 30, samples are called small. The theory of small samples is treated under “Small Sampling Theory”.

Much of the above excerpted from Murray R. Spiegel. Statistics. Schaum.

For examples, worked problems, and clarification see Theory and Problems of Statistics by Murray R. Spiegel, Schaum’s Outline Series, Schaum Publishing Co.

References

Murray R Spiegel. Statistics (Schaum Publishing Co.)