Binomial, Normal, Poisson, and Multinomial Distributions

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

Binomial distribution

Bernoulli experiment. An experiment or trial for which there are two possible outcomes, such as “heads” or “tails” when tossing a coin, or “A” or “B” when asking if candidate A or B is favored.

James/James Mathematics Dictionary

Problem. Suppose we toss a fair coin ten times and ask, “What is the probability that the coin will come up heads exactly 7 times in the ten tosses?” Solution. Each toss is a Bernoulli experiment and the ten tosses represent ten independent Bernoulli experiments. The answer is given by the following theorem.

Theorem. Let X is the number of successes in n independent Bernoulli experiments. Then the range of X is the set {0, 1, ... , n}. Let the probability of success in a single experiment be p. Then the probability of exactly k successes in n experiments is given by

1) P(X = k) = _nC_kp^kq^n-k

where q = 1 - p and _nC_k = n! / [k!(n-k)!]. Here _nC_k corresponds to the coefficients in the expansion of (x + y)ⁿ. _nC_k also represents the number of combinations of n things taken k at a time.

Derivation

In the above X is said to be binomially distributed or a binomial random variable.

To continue: Suppose we toss a coin ten times and ask, “What is the probability that the coin will come up heads exactly 7 times in the ten tosses?” Solution. Each toss is a Bernoulli experiment and the ten tosses represent ten independent Bernoulli experiments. Here p = ½ and q = ½. The answer from 1) above is given by P(X = 7) = ₁₀C₇p⁷q³ = {10! / [7!(3)!}{(½)⁷(½)³}

Example 1. The probability of getting at least 4 heads in 6 tosses of a fair coin is

₆C₄(½)⁴(½)^6-4 + ₆C₅(½)⁵(½)^6-5 + ₆C₆(½)⁶ = 15/64 + 6/64 + 1/64 = 11/32

The binomial distribution. The discrete probability distribution

P(X = k) = _nC_kp^kq^n-k

(See Fig. 1) is often called the binomial distribution since for X = 0, 1, 2, .... , n it corresponds to the successive terms in the binomial formula or binomial expansion

2) (q + p)ⁿ = qⁿ + _nC₁q^n-1p + _nC₂q^n-2p² + .... + pⁿ

where 1, _nC₁, _nC₂, .... are called the binomial coefficients.

Example. (q + p)⁴ = q⁴ + ₄C₁q³p + ₄C₂q²p² + ₄C₃qp³ + p⁴

= q⁴ + 4q³p + 6q²p² + 4qp³ + p⁴

Example 2. If a coin is tossed three times, then n = 3, the probability of a head is p = ½, q = ½, the range of X is the set {0, 1, ... , 3} and the probabilities of 0, 1, 2 or 3 heads are ⅛, ⅜, ⅜, ⅛. These four numbers ⅛, ⅜, ⅜, ⅛ are the terms in the expansion of (½ + ½)³ by the binomial theorem.

In general,

The binomial distribution is also called the Bernoulli distribution after James Bernoulli who discovered it at the end of the 17^th century.

The mean of the binomial distribution is np, the variance is npq, and the moment generating function is M(t) = (q + pe^t)ⁿ. When n is large, the binomial distribution can be approximated by a normal distribution with mean np and variance npq. The binomial distribution can be approximated by a Poisson distribution with mean np if n is large.

Normal distribution

The normal distribution. One of the most important distributions is a continuous probability distribution called the normal distribution defined by

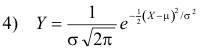
where μ = mean, σ = standard deviation, π = 3.14159... , e = 2.71828...

The total area bounded by the curve 4) and the x axis is one. The area under the curve between the two ordinates X = a and X = b, where a < b, represents the probability that X lies between a and b and is denoted by Pr{a<X<b}.

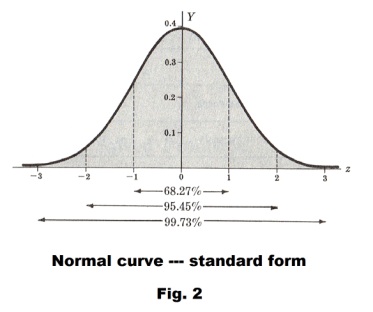
When the variable X is expressed in terms of standard units, z = (X - μ)/σ, equation 4) is replaced by the so-called standard form

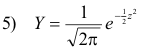
In this case we say that z is normally distributed with mean zero and variance one.

See Fig. 2. The areas included between z = -1 and z = 1, z = -2 and z = 2, and z = -3 and z = 3 are equal respectively to 68.27%, 95.45% and 99.73% of the total area which is one.

Tables exist which give the area under this curve between the ordinate at z = 0 and the ordinate at any positive value of z. Using such a table the area between any two ordinates can be found.

Relationship between binomial and normal distributions. If n is large and if neither p nor q is too close to zero, the binomial distribution can be closely approximated by a normal distribution with a standardized variable given by

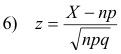
The approximation becomes better with increasing n, and in the limiting case is exact. Examination of the formulas in tables 1 and 2 shows that as n increases the skewness and kurtosis of the binomial distribution approaches that of the normal distribution.

Poisson Distribution

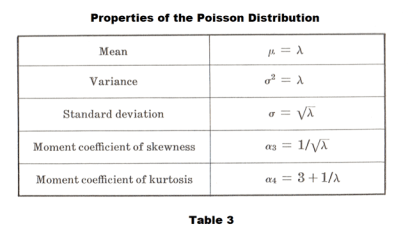
Poisson Distribution. The discrete probability distribution

where e = 2.71828... and λ is a given constant, is called the Poisson distribution, after Poisson who discovered it in the early part of the 19^th century.

Relationship between the Binomial and the Poisson distributions. In the binomial distribution, if n is large while the probability p of occurrence of an event is close to zero so that q = (1 - p) is close to 1, the event is called a rare event. In practice we consider an event as rare if the number of trials is at least 50 while np is less than 5. In the case of rare events the binomial distribution the binomial distribution is very closely approximated by the Poisson distribution with λ = np. This is seen by setting λ = np in Table 3 and remembering q ≈ 1 and p ≈ 0 in Table 1.

Since there is a relationship between the binomial and normal distributions, it follows that there is also a relationship between the Poisson and normal distributions. It can be shown that the Poisson distribution approaches a normal distribution with standardized variable as λ →∞ .

Multinomial distribution

Multinomial distribution. If events E₁, E₂, .... ,E_k can occur with probabilities p₁, p₂, .... ,p_krespectively, then the probability that E₁, E₂, .... ,E_k will occur X₁, X₂, .... , X_k times respectively is

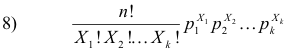
where X₁ + X₂ + .... + X_k = n .

This distribution, which is a generalization of the binomial distribution is called the multinomial distribution since 8) is the general term in the multinomial expansion (p₁ + p₂ + .... + p_k)ⁿ .

Example. If a fair die is tossed 12 times, the probability of getting 1, 2, 3, 4, 5 and 6 points exactly twice each is

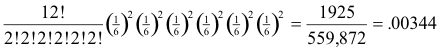
The expected numbers of times that E₁, E₂, .... ,E_k will occur in n trials are np₁, np_2, .... np_k respectively.

Multinomial experiment. A multinomial experiment is an experiment that has the following properties:

1. The experiment consists of n identical trials.

2. There are k possible outcomes. Each trial results in one of the k outcomes.

3. On any given trial, the probability that a particular outcome will occur is constant.

4. The trials are independent; that is, the outcome on one trial does not affect the outcome on other trials.

Consider the following statistical experiment. You toss two dice three times, and record the outcome on each toss. This is a multinomial experiment because:

1) The experiment consists of repeated trials. We toss the dice three times.

2) Each trial can result in a discrete number of outcomes - 2 through 12.

3) The probability of any outcome is constant; it does not change from one toss to the next.

4) The trials are independent; that is, getting a particular outcome on one trial does not affect the outcome on other trials.

Note: A binomial experiment is a special case of a multinomial experiment. The main difference is as follows: With a binomial experiment, each trial can result in two - and only two - possible outcomes. With a multinomial experiment, each trial can have two or more possible outcomes.

References

Murray R Spiegel. Statistics (Schaum Publishing Co.)

James/James. Mathematics Dictionary