Website owner: James Miller
Elementary probability theory. Conditional probability. Independent and dependent events. Mutually exclusive events. Discrete probability distributions. Continuous probability distributions. Mathematical expectation. Combinatorial analysis. Permutations. Combinations. Binomial Formula.
Definitions of probability
Following are two generally used definitions of probability:
1. Classical definition of probability. Suppose an event E can happen in h ways out of a total of n possible equally likely ways. Then the probability of occurrence of the event (called its success) is denoted by p or Pr{E} and is defined as
p = h/n
The probability of non-occurrence of the event (called its failure) is denoted by q or Pr{not E} and is defined as
q = (n - h)/n = 1 - h/n = 1 - p
Thus p + q = 1 Pr[E} + Pr{not E} = 1
Example 1. If one ball is drawn from a bag containing two white balls and five black balls, and each ball is equally likely to be drawn, then the probability of drawing a white ball is 2/7 and the probably of drawing a black ball is 5/7.
The probability of an event is a number between 0 and 1. If an event cannot occur, its probability is 0.
Odds in favor of an event. If p is the probability that an event will occur, the odds in favor of it happening are p:q (read “p to q”); the odds against it happening are q:p. Thus the odds of drawing a white ball from the bag of Example 1 are p:q = 2/7:5/7 = 2 to 5.
2. Relative frequency definition of probability. If, in a random sequence of n trials of an event with h favorable outcomes, the ratio h/n as n increases indefinitely has the limit p, then p is the probability of the event h.
Conditional probability. Independent and dependent events.
Conditional probability. If E1 and E2 are two events, the probability that E2 occurs given that E1 has occurred is denoted by Pr{E2|E1} or Pr{E2 given E1} and is called the conditional probability of E2 given that E1 has occurred.
Independent and dependent events. If the occurrence or non-occurrence of E1 does not affect the probability of occurrence of E2, then Pr{E2|E1} = Pr{E2} and we can say that E1 and E2 are independent events; otherwise they are dependent events.
If we denote by E1E2 the event that “both E1 and E2 occur”, sometimes called a compound event, then
1) Pr{E1 E2} = Pr{E1}Pr{E2|E1}
For three events E1, E2, E3 we have
2) Pr{E1 E2 E3} = Pr{E1}Pr{E2|E1}Pr{E3|E1E2}
For the case where E1, E2, E3 are all independent events
3) Pr{E1 E2} = Pr{E1}Pr{E2}
4) Pr{E1 E2 E3} = Pr{E1}Pr{E2}Pr{E3}
In general if E1, E2, E3, .... , En are n independent events having respective probabilities p1, p2, p3, ... , pn, then the probability of occurrence of E1 and E2 and E3 and .... En is p1 p2 p3 ... pn.
Example 1. Let E1 and E2 be the events “heads on second toss” and “heads on fifth toss” of a coin, respectively. E1 and E2 are independent events, so that the probability of heads on both the second and fifth tosses is, assuming the coin is fair,
Pr{E1 E2} = Pr{E1}Pr{E2} = (½)(½) = ¼
Example 2. If the probability that A will be alive in 15 years is 0.8 and the probability that B will be alive in 15 years is 0.3, then the probability that both will be alive in 15 years is (0.8)(0.3) = 0.24.
Example 3. Suppose a box contains 5 white balls and 3 black balls. Let E1 be the event “first ball drawn is black” and E2 be the event “second ball drawn is black” where balls are not replaced after being drawn. Here E1 and E2 are dependent events. The probability that the first ball drawn is black is Pr{E1} = 3/(5+3) = 3/8. The probability that the second ball drawn is black is Pr{E2|E1} = 2/7. Then the probability that both balls drawn are black is 3/8⋅2/7 = 3/28.
Mutually exclusive events. Two or more events are called mutually exclusive if the occurrence of any one of them excludes the occurrence of the others. Thus if E1 and E2 are mutually exclusive events, Pr{E1 E2} = 0.
If E1 + E2 denotes the event that “either E1 or E2 or both occur”, then
5) Pr{E1 + E2} = Pr{E1} + Pr{E2} - Pr{E1 E2}
In particular, for mutually exclusive events:
6) Pr{E1 + E2} = Pr{E1} + Pr{E2}
In general, if E1, E2, .... , En, are mutually exclusive events having respective probabilities of occurrence p1, p2, p3, ... , pn, then the probability of occurrence of either E1 or E2 or ... En is p1 + p2 + p3 + ... + pn.
Example 1. If E1 is the event “drawing a ace from a deck of cards” and E2 is “drawing a king”, then Pr{E1} = 4/52 = 1/13 and Pr{E2} = 4/52 = 1/13. The probability of drawing either an ace or a king in a single draw is
Pr(E1 + E2} = Pr{E1} + Pr{E2} = 1/13 + 1/13 = 2/13
since both ace and king cannot be drawn in a single draw and are thus mutually exclusive events.
Example 2. If E1 is the event “drawing an ace” from a deck of cards and E2 is the event “drawing a spade”, then E1 and E2 are not mutually exclusive since the ace of spades can be drawn. Thus the probability of drawing either an ace or a spade or both is
Pr(E1 + E2} = Pr{E1} + Pr{E2} - Pr{E1 E2} = 4/52 + 13/52 - 1/52 = 16/52 = 4/13
Discrete probability distributions
Discrete probability distribution. If a variable X can assume a discrete set of values X1, X2, X3, ... , Xk with respective probabilities p1, p2, p3, ... , pk where p1 + p2 + p3 + ... + pk = 1, we say that a discrete probability distribution has been defined. The function p(X) which has the respective values p1, p2, p3, ... , pk for x = X1, X2, X3, ... , Xk, is called the probability function or frequency function of X. Because X can assume certain values with given probabilities, it is often called a discrete random variable. A random variable is also known as a chance variable or stochastic variable.
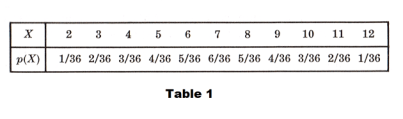
Example. Let a pair of dice be tossed and let X denote the sum of the points obtained. The probability distribution is shown in Table 1. A very large number of tosses should give approximately the numbers shown in the table. For example, the table shows the probability of getting the sum X = 5 as 4/36 = 1/9. Thus in 900 tosses of the dice we would expect around 1/9 × 900 = 100 tosses to give the sum 5.

Note that this discrete probability distribution of X is analogous to a relative frequency distribution with probabilities replacing relative frequencies. Thus we can think of probability distributions as theoretical or ideal limiting forms of relative frequency distributions when the number of observations is made very large. For this reason we can think of probability distributions as being distributions for populations, whereas relative frequency distributions are distributions of samples drawn from the population.
The probability distribution can be represented graphically by plotting p(X) against X, as for frequency distributions.
By cumulating probabilities we obtain cumulative probability distributions which are analogous to cumulative relative frequency distributions. The function associated with this distribution is sometimes called a distribution function.
Continuous probability distributions

The above ideas can be extended to the case where the variable X may assume a continuous set of values. The relative frequency polygon of a sample becomes, in the theoretical or limiting case of a population, a continuous curve such as that shown in Fig 1, whose equation is Y = p(X). The total area under this curve bounded by the X axis is equal to one, and the area under the curve between lines X = a and X = b (shaded in the figure) gives the probability that X lies between a and b (which can be denoted by Pr{a<X<b).
We call p(X) a probability density function, or briefly a density function. When such a function is given we say that a continuous probability distribution for X has been defined. The variable X is then often called a continuous random variable.
As in the discrete case, we can define cumulative probability distributions and the associated distribution functions.
Mathematical expectation. If a variable X can assume a discrete set of values X1, X2, X3, ... , Xk with respective probabilities p1, p2, p3, ... , pk where p1 + p2 + p3 + ... + pk = 1, the mathematical expectation of X is defined as
7) E(X) = p1X1 + p2X2 + .... + pkXk
Syn. Expected value
Example. Two coins are tossed and John receives $5 if they both show heads, $1 if one shows heads and one shows tails, and pays $6 if both show tails. His expectation is 5⋅¼ + 1⋅½ + (-6)⋅¼ = ¼ dollars
Relation between population and sample mean. If we select a sample of size N at random from a population it is possible to show that the expected value of the sample mean m is the population mean μ.
Combinatorial analysis
Fundamental principle. If an event can happen in any one of m ways and after this has occurred another event can happen in any one of n ways, then the number of ways in which both events can happen in the specified order is mn ways.
Example 1. Q. In walking from point A to point B one can take any one of three roads. In going from point B to point C he has a choice of four roads. By how many different routes can he walk from A to C? A. 3×4 = 12 different routes.
Example 2. Q. At a restaurant one is offered a choice of four meat courses and five deserts. In how many ways can he select a meal consisting of a meat course and a desert? A. 4×5 = 20 ways.
Def. Permutation. An ordered arrangement or sequence of all or part of a set of things. If we are given a set of n different objects and arrange r of them in a definite order, such an ordered arrangement is called a permutation of the n objects r at a time. For example, the permutations of the three letters a, b, c taken all at a time are abc, acb, bca, bac, cba, cab. Each of these represents a separate permutation of the letters a, b, c. The permutations of the three letters a, b, c taken two at a time are ab, ac, ba, bc, ca, cb.
The number of permutations that can be formed in a particular situation is found by using the Fundamental Principle stated above.
Example 1. How many permutations of four letters can be formed from the letters a, b, c, d, e, f, g?
Solution. Seven letters can be put in the first position, then six letters can be put in the second position, then five letters can be put in the third position, then four letters can be put in the fourth position. Thus the answer is 7·6·5·4 = 840.
Example 2. How many integers of four figures can be formed from the nine digits 1, 2, 3, 4, 5, 6, 7, 8, 9 if none is used twice?
Solution. Nine numbers can be put in the first position, then eight numbers can be put in the second position, then seven numbers can be put in the third position, then six numbers can be put in the fourth position. Thus the answer is 9·8·7·6 = 3024
The number of permutations of n things taken r at a time is denoted by nPr.
Theorem 1. The number of permutations of n different things taken r at a time is
nPr = n(n-1)(n-2) ... (n - r + 1)
Note that the product n(n-1)(n-2) ... (n - r + 1) in the right member contains exactly r factors.
Factorial notion. If n is a positive integer, the symbol n!, which is read “n factorial” or “factorial n,” denotes the product of the first n integers:
n! = 1·2·3· ... ·n
This definition of factorial leaves the case when n is zero meaningless. In order to make certain formulas valid in all cases, factorial zero is arbitrarily defined to be 1.
Example. 5! = 1·2·3·4·5 = 120
Theorem 2. The number of permutations of n different things taken all at a time is
nPn = n(n-1)(n-2) ... 1 = n!
Circular permutations.
Theorem 3. The number of ways of arranging n different objects around a circle is (n - 1)! ways.
Number of permutations of n things with some things alike. The letters of the word formula are all different and thus can be arranged in 7! distinct ways. However, in the word between there are three letters that are alike and thus cannot be distinguished from each other in any arrangement that we make. It is obvious that the number of distinct permutations of the letters in the word between will be less than 7!. How many distinct permutations can be made from the word between? Using the following theorem we find it is 7! / 3!.
Theorem 4. Given n objects, of which k1 are alike, k2 others are alike, k3 others are alike, etc.; The number of different permutations that can be made of the n objects taking them all at a time is

Def. Combination. A combination of a set of objects is any subset without regard to order. If we are given a set of n objects, any selection or set of r of the objects, considered without regard to their arrangement, is a combination of the n objects r at a time.
Example. The combinations of the letters a, b, c taken two at a time are ab, ac, bc. We note that ab and ba are two permutations but one combination.
The number of combinations of n things taken r at a time is denoted by nCr.
Theorem 5. The number of combinations of n things taken r at a time is
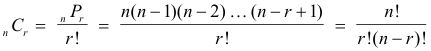
Note that nCr = nCn-r .
Theorem 6. The total number of combinations of n things taking them any number at a time (i.e. 1, 2, 3, ... , n at a time) is given by
nC1 + nC2 + nC3 + ..... + nCn = 2n - 1
Binomial Formula. If n is a positive integer
![]()
which can also be written as
2) (x + y)n = xn + nC1xn-1y + nC2xn-2y2 + nC3xn-3y3 + ..... + yn

Pascal’s Triangle. To the right is pictured the first 11 rows of Pascal’s Triangle. The triangle is formed as follows: The first and last numbers of each row is a 1. Each number in the interior of the triangle is the sum of the two numbers to the right and left above it. We thus work down from the top computing the numbers of each row from the numbers above it.
Connection between Pascal’s triangle and Binomial Formula. The coefficients on the right side of 2) are precisely the numbers on row n of Pascal’s Triangle (the first row is 1 1, the second row is 1 2 1, etc. — neglecting the 1 at the top vertex)
The binomial formula also holds for negative and fractional values of n. However, when n is a negative or fractional number the expansion does not terminate. In this case it is an infinite series called the binomial series. Such an expansion converges and its sum is (x + y)n if |y| < |x|, or if x = y ≠0 and n > -1, or if x = -y ≠0 and n > 0.
Stirling’s approximation to n!
When n is large a direct evaluation of n! is impractical. In such case use is made of an approximation formula due to Stirling:
![]()
where e = 2.71828 ...is the natural base of logarithms.
Application of point set theory to probability theory
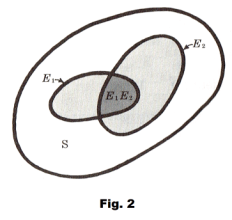
In modern probability theory we think of all possible outcomes or results of an experiment, game, etc., as points in a space (which may be of one, two, three, or more dimensions) called a sample space S. If S contains only a finite number of points then we can associate with each point a non-negative number, called a probability, such that the sum of all numbers corresponding to all points in S add to one. A event is a set or collection of points in S as indicated by E1 or E2 in Fig. 2, called an Euler diagram or Venn diagram.
The event E1 + E2 is the set of points which are either in E1 or E2 or both, while the event E1E2 is the set of points common to both E1 and E2. The probability of an event such as E1 is the sum of the probabilities associated with all of the points contained in the set E1. Similarly the probability of E1 + E2 denoted by Pr{E1 + E2}, is the sum of the probabilities associated with all of the points contained in the set E1 + E2. If E1 and E2 have no points in common, i.e. the events are mutually exclusive, then Pr{E1 + E2} = Pr{E1} + Pr{E2}. If they have points in common then Pr{E1 + E2} = Pr{E1} + Pr{E2} - Pr{E1 E2}.
The set E1 + E2 is sometimes denoted by E1∪E2 and is called the union of the two sets. The set E1E2 is sometimes denoted by E1∩E2 and is called the intersection of the two sets. Extensions to more than two sets can be made. Thus instead of E1 + E2 + E3 and E1E2E3 we could use the notation E1∪E2∪E3 and E1∩E2∩E3 respectively.
A special symbol ∅ is sometimes used to denote a set with no points in it, called the null set. The probability associated with an event corresponding to this set is zero i.e. Pr{∅} = 0. If E1 and E2 have no points in common, we can write E1E2 = ∅, which means that the corresponding events are mutually exclusive and Pr{E1E2} = 0.
____________________________________________________________________________
Summary of conventions
E1E2 represents the event that “both E1 and E2 occur”
E1E2 is sometimes denoted by E1∩E2 and is called the intersection of the two sets.
E1 + E2 denotes the event that “either E1 or E2 or both occur”
The set E1 + E2 is sometimes denoted by E1∪E2 and is called the union of the two sets.
Pr{E2|E1} or Pr{E2 given E1} denotes the probability that E2 occurs given that E1 has occurred
____________________________________________________________________________
References
Murray R Spiegel. Statistics (Schaum Publishing Co.)
James/James. Mathematics Dictionary
Jesus Christ and His Teachings
Way of enlightenment, wisdom, and understanding
America, a corrupt, depraved, shameless country
On integrity and the lack of it
The test of a person's Christianity is what he is
Ninety five percent of the problems that most people have come from personal foolishness
Liberalism, socialism and the modern welfare state
The desire to harm, a motivation for conduct
On Self-sufficient Country Living, Homesteading
Topically Arranged Proverbs, Precepts, Quotations. Common Sayings. Poor Richard's Almanac.
Theory on the Formation of Character
People are like radio tuners --- they pick out and listen to one wavelength and ignore the rest
Cause of Character Traits --- According to Aristotle
We are what we eat --- living under the discipline of a diet
Avoiding problems and trouble in life
Role of habit in formation of character
Personal attributes of the true Christian
What determines a person's character?
Love of God and love of virtue are closely united
Intellectual disparities among people and the power in good habits
Tools of Satan. Tactics and Tricks used by the Devil.
The Natural Way -- The Unnatural Way
Wisdom, Reason and Virtue are closely related
Knowledge is one thing, wisdom is another
My views on Christianity in America
The most important thing in life is understanding
We are all examples --- for good or for bad
Television --- spiritual poison
The Prime Mover that decides "What We Are"
Where do our outlooks, attitudes and values come from?
Sin is serious business. The punishment for it is real. Hell is real.
Self-imposed discipline and regimentation
Achieving happiness in life --- a matter of the right strategies
Self-control, self-restraint, self-discipline basic to so much in life