Arithmetic mean. Median. Mode. Geometric mean. Harmonic mean. Root mean square or quadratic mean.

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

Arithmetic mean. Median. Mode. Geometric mean. Harmonic mean. Root mean square or quadratic mean

Mean, Median, Mode, and other measures of central tendency

Arithmetic mean. The arithmetic mean of n numbers is their sum divided by n. The arithmetic mean is commonly called the average. In symbols, the arithmetic mean a of the n numbers a₁, a₂, ... , a_n is

1) a = (a₁ + a₂, + ... + a_n)/n

If the numbers a₁, a₂, ... , a_k occur f₁, f₂. ... , f_k times respectively (i.e. occur with frequencies f₁, f₂. ... , f_k ), the arithmetic mean is

2) a = (a₁ f₁ + a₂ f₂, + ... + a_k f_k) / (f₁ + f₂ + ... + f_k)

Weighted arithmetic mean. If we associate with the numbers a₁, a₂, ... , a_k certain weighting factors (or weights) w₁, w₂. ... , w_kthe weighted arithmetic mean is (by definition)

3) a = (a₁ w₁ + a₂ w₂, + ... + a_k w_k) / (w₁ + w₂ + ... + w_k)

By comparing 2) and 3) we see that 2) is the weighted arithmetic mean of k numbers a₁, a₂, ... , a_k with weights f₁, f₂. ... , f_k .

Properties of the arithmetic mean. The arithmetic mean has the following properties:

1. The algebraic sum of the deviations of a set of numbers from their arithmetic mean is zero.

2. The sum of the squares of the deviations of a set of numbers a₁, a₂, ... , a_k from any number x is a minimum if an only if x = a (where a is the average).

3. If f₁ numbers have mean m₁, f₂ numbers have mean m₂, ..... , f_k numbers have mean m_k , then the mean of all the numbers is

4) a = (f₁ m₁ + f₂ m₂ +..... + f_k m_k ) / (f₁ + f₂ + ... + f_k)

i.e. a weighted mean of all the means.

4. Given n numbers a₁, a₂, ... , a_n. If x is any guessed (or assumed) arithmetic mean of the numbers (which may be any number) and if d_i = a_i - x are the deviations of a_i from x, then equations 1) and 2) for the average a become

5) a = x + (Σd_i)/n

6) a = x + (Σf_id_i)/n

where n = Σf_i

Arithmetic mean computed from grouped data

When data are presented in a frequency table all values falling in a particular class interval are considered as coincident with the class mark (or midpoint) of the interval. Formulas 2) and 6) are valid for such grouped data if we interpret a_i as the class mark, f_i its corresponding class frequency, x any guessed or assumed class mark, and d_i = a_i - x the deviations of a_i from x.

Computations using formulas 2) and 6) are sometimes called the long and short methods respectively.

If class intervals all have equal size c, the deviations d_i = a_i - x can all be expressed as cu_i where u_i can be positive or negative integers or zero and formula 6) becomes

7) a = x + c(Σf_iu_i)/n

which is equivalent to the equation a = x + cu.

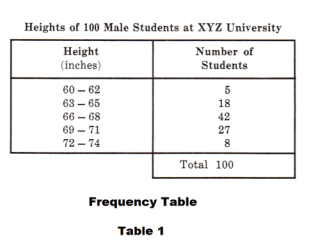
This is called the coding method for computing the mean. It is a very short method and should always be used for grouped data when the class interval sizes are equal. Table 1 shows a frequency table for the heights of 100 male students at XYZ University and Table 2 shows the computation of the average height using the coding method.

Median. The median of a set of n numbers is the middle number when the numbers are arranged in order of size; or if there is no middle number (as when there is an even number of numbers), the average of the two middle numbers.

Example 1. The set of numbers 2, 5, 6, 8, 9, 11, 15 , 16, 22 has a median 9.

Example 2. The set of numbers 5, 8, 9, 11, 13, 17, 20, 24 has a median ½(11 + 13) = 12

For grouped data the median, obtained by interpolation, is given by

8) Median = L₁ + ( (N/2 - (Σf)₁) / f_median ) c

where

L₁ = lower class boundary of the median class (i.e. the class containing the median)

N = total number of items in the data (total of all frequencies)

(Σf)₁ = sum of frequencies of all classes lower than the middle class

f_median = frequency of median class

c = size of median class interval

The median is the value of x (abscissa) corresponding to that vertical line that divides a histogram into two parts with equal areas.

Mode. The mode of a set of n numbers is that value that occurs with the greatest frequency.

The mode may or may not exist and if it does exist it may not be unique.

Example 1. The set 2, 2, 3, 4, 5, 5, 6, 6, 6, 7, 7, 8, 8, 9 has the mode 6.

Example 2. The set 2, 3, 5, 7, 8, 9, 10, 12 has no mode.

Example 3. The set 3, 4, 5, 5, 5, 6, 6, 7, 8, 8, 8, 10, 11 has two modes, 5 and 8, and is called bimodal.

A distribution having only one mode is called unimodal.

In the case of grouped data where a frequency curve has been constructed to fit the data, the mode is the value (or values) of X corresponding to the maximum point (or points) on the curve.

Empirical relation between the mean, median, and mode

For unimodal curves that are moderately skewed (asymmetrical), the following empirical relation obtains:

9) Mean - Mode = 3 (Mean - Mode)

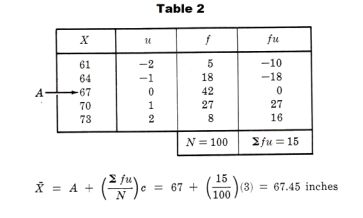
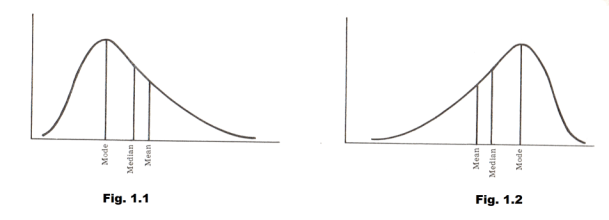
Figures 1.1 and 1.2 show the relative positions of the mean, median, and mode for frequency curves that are skewed to the right and left respectively. For symmetrical curves the mean, median, and mode all coincide.

The geometric mean

The geometric mean G of a set of n numbers a₁, a₂, ... , a_n is the n-th root of the product of the numbers:

For the case of grouped data let us suppose the numbers a₁, a₂, ... , a_k occur with frequencies f₁, f₂. ... , f_k where f₁ + f₂ + ... + f_k = n is the total frequency. Then

The harmonic mean

The harmonic mean H of a set of n numbers a₁, a₂, ... , a_n is the reciprocal of the arithmetic mean of the reciprocals of the numbers:

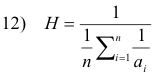
For the case of grouped data, if x₁, x₂, x_{3, ....}represent the class marks in a frequency distribution with corresponding class frequencies f₁, f₂, f₃ ... respectively, then the harmonic mean H of the distribution is given by

where n = f₁ + f₂ + f₃ + ... = Σf

The root mean square or quadratic mean

The root mean square or quadratic mean of a set of numbers a₁, a₂, ... , a_n is defined by

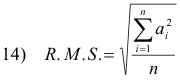
Quartiles, deciles, and percentiles

If a set of data is arranged in order of magnitude, the middle value (or arithmetic mean of the two middle values) which divides the data into two equal parts is the median. Similarly, The three values that divide the data into four equal parts are called quartiles and are denoted by Q₁, Q₂, and Q₃ and called the first, second and third quartiles. In a similar way the values that divide the data into ten equal parts are called deciles and denoted by D₁, D₂, .... , D₉and the values that divide the data into one hundred equal parts are called percentiles and are denoted by P₁, P₂, .... , P₉₉.

Problem. Find the quartiles, Q₁, Q₂, and Q₃ for the wages of the 65 employees at JET Company as shown in the frequency table of Table 3.

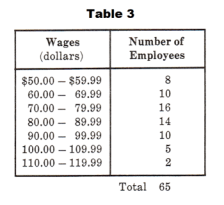
Solution. The first quartile Q₁ is that wage obtained by counting 65/4 = 16.25 of the cases beginning with the first (lowest) class. Since the first class contains 8 cases, we must take 8.25 (16.25 - 8) of the 10 cases from the second class. Making the assumption that wages increase linearly as we go from the bottom to the top of each class, we compute the answer as

Q₁ = $59.995 + ($10.00)(8.25/10) = $68.25

The second quartile is the wage obtained by counting the first 65/2 = 32.5 of the cases. Since the first two cases comprise 18 cases, we must take 32.5 - 18 = 14.5 of the 16 cases of the third class. Thus

Q₂ = $69.995 + ($10.00)(14.5/16) = $79.06

We note that Q₂ is actually the median.

The third quartile is obtained by counting the first ¾ of the 65 cases i.e. ¾(65) = 48.75 cases. Since the first four classes comprise 48 cases, we must take 48.75 - 48 = 0.75 cases of the 10 cases of the fifth class. Thus

Q₃ = $89.995 + ($10.00)((0.75/10) = $90.75

Thus 25% of the employees earn $68.25 or less, 50% earn $79.06 or less, and 75% earn $90.75 or less.