Concept of an operator. Examples of linear operators. Integral operator. Bounded, adjoint operators.

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

Concept of an operator. The term “operator” is another term for function, mapping or transformation. An operator assigns an object from one set (the co-domain) to an object from another set (the domain). If we are talking about vector spaces we think of an operator as “operating” on one vector to produce another vector. It is viewed as a kind of black box that operates on vectors to produce other vectors. The black box has an input and an output. We input a vector into the box and it then outputs a vector. An example is the matrix A in the matrix equation y = Ax where A is viewed as a black box that operates on the vector x to produce vector y. Here matrix A maps a vector x from one space (the domain) into the vector y in another space (the co-domain). If we are talking about functional spaces where a function f(x) is viewed as a vector, an operator is viewed as a black box that operates on a function to produce another function. The input to the box is a function and the output is another function.

Example:

which associates with function f a certain function g (where K(x, t) is a definite known function called the kernel).

Def. Linear operator. Let an operator A be defined on a vector space. It is linear if

A(av₁ + bv₂) = aAv₁ + bAv₂

for all vectors v₁ and v₂ and scalars a, b.

Examples of linear operators (or linear mappings, transformations, etc.) .

1. The mapping y = Ax where A is an mxn matrix, x is an n-vector and y is an m-vector. This represents a linear mapping from n-space into m-space.

2. The mapping y = Ax where A is an nxn matrix, x is an n-vector and y is an n-vector. This represent a linear mapping from n-space into n-space.

3. Let V be the vector space of all n-square matrices over the real field R and A be an n-square matrix over R.. Let v be any member of V. The transformation

w = Av

where w V, constitutes a linear transformation T: V → V.

4. Let V be the vector space of all polynomials in the variable x over the real field R. Then the derivative defines a linear transformation D: V → V where, for any polynomial f V, we let D(f) = df/dx. For example, D(4x² + 3x + 5) = 8x + 3.

5. Let V be the vector space of all polynomials in the variable x over the real field R. Then the integral from, say, 0 to 1, defines a linear transformation T: V → R where, for any polynomial

f V, we let

For example,

6. Let V be the vector space of all real-valued continuous functions defined on the interval [0,1]. Then for any f V the transformation

defines a linear transformation T : V → V.

7. Let V be the vector space of all real-valued continuously differentiable functions defined on the interval [0,1] and W be the vector space of all real-valued continuous functions defined on the interval [0,1]. Then for any f V the transformation

D(f) = f '(x)

defines a linear transformation D:V → W.

8. The integral operator

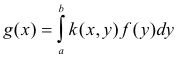
which associates with function f a certain function g (where k(x, y) is a definite known function called the kernel).

Def. Integral operator. A linear operator that associates with every function f another function g by means of an integral equation.

Example. The formula

associates with every function f a certain function g. Symbolically, we can write this transformation as

g = Af

where the operator A is called an integral operator. For each vector f that A is provided, it gives a vector g. We can view it as a mapping where A maps each vector f into a vector g.

Def. Bounded operator. An operator A is called bounded if a positive real number C exists such that

|| Av || < C ||v||

Theorem. Let A be a bounded linear operator which maps a Hilbert space H into H (with the domain of A equal to H). Then a uniquely determined bounded linear operator A*, called the adjoint of A, exists such that the inner products (Af, g) and (f, A*g) are equal for all f, g ε H. If A = A*, the operator is called self-adjoint.

References

James & James. Mathematics Dictionary

Mathematics, Its Content, Methods and Meaning. Vol. 3, Chap. XIX