Website owner: James Miller
Solution of linear systems by determinants. Properties of determinants. Evaluation of determinants. Minor. Cofactor. Cramer’s Rule. Homogeneous systems.
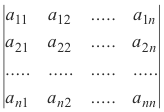
Def. Determinant. A square array of quantities, called elements, symbolizing the sum of certain products of these elements. The symbol

denotes a determinant of order n. It is an abbreviation for the algebraic sum of all possible products
![]()
where each product of n factors contains one and only one element from each row and one and only one element from each column. There will be n! such products. Each product has a plus or minus sign attached to it according as the column indices form an even or odd permutation when the row indices are in natural order (i.e. 1, 2, 3, ... ). For example, the term a13a21a34a42 of the expansion of a determinant of order four has the column indices in order (3,1,4,2) . This term should have a negative sign attached, since three successive interchanges will change the column indices to (1,3,4,2), (1,3,2,4) and (1,2,3,4), the last being in natural order.
Determinants of the second order. The value of the determinant
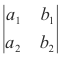
of order two is given by
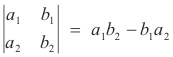
The solution of a system of two linear equations in two unknowns given in terms of determinants. The solution of the linear system
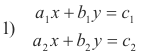
is
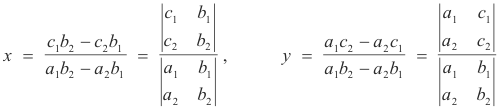
providing the equations are consistent and independent. The equations are consistent and independent if and only if
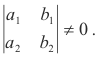
Note that the denominator determinants are the same for both x and y and consist of the coefficients of the variables x and y arranged exactly as they appear in the left members of 1). This denominator determinant is called the determinant of the coefficients or the determinant of the system. The numerator determinants are constructed from this denominator determinant by replacing the column containing the coefficients of the variable being solved for by the column of constants, c1 and c2, from the right side of 1) i.e. the numerator determinant in the solution for x is constructed from the denominator determinant by replacing the coefficients a1 and a2 of x by c1 and c2 and likewise in the solution for y.
Determinants of the third order. The value of the determinant

is given by
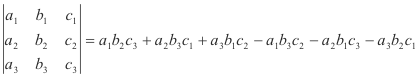
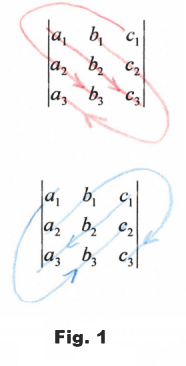
This sum can be remembered by the device shown in Fig. 1 where elements connected by red lines correspond to positive products and elements connected by blue lines represent negative products.
The solution of a system of three linear equations in three unknowns given in terms of determinants. The solution of the linear system
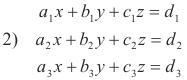
is given by
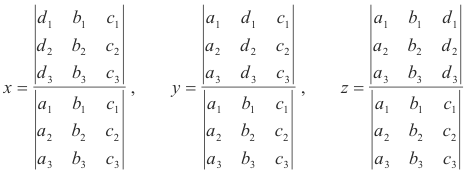
providing the equations are consistent and independent. The equations are consistent and independent if and only if
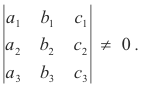
Determinants are most easily evaluated by a technique employing the following properties of determinants.
Properties of determinants.
1. If all the elements of a column (or row) are zero, the value of the determinant is zero.
2. If each of the elements in a row (or column) of a determinant is multiplied by the same number p, the value of the determinant is multiplied by p.
3. If two columns (or rows) are identical, the value of the determinant is zero.
4. Interchanging any two rows (or columns) reverses the sign of the determinant.
5. The value of a determinant is unaltered when all the corresponding rows and columns are interchanged. Thus any theorem proved true for rows holds for columns, and conversely.
Example.
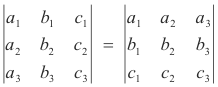
6. If each element of a row (or column) of a determinant is expressed as the sum of two (or more) terms, the determinant can be expressed as the sum of two (or more) determinants.
Example.
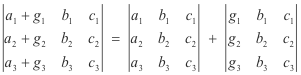
7. If to each element of a row (or column) of a determinant is added m times the corresponding element of another row (or column) the value of the determinant is not changed.
Def. Minor of an element in a determinant. The determinant, of next lower order, obtained by striking out the row and column in which the element lies.
Def. Cofactor of an element in a determinant. Denote the minor of element aij of the i-th row and j-th column of a determinant |A| by |Mij |. The cofactor αij of the element aij is given as the signed minor (-1)i+j |Mij | i.e. it is the minor, taken with a positive or negative sign, according as the sum of the column number and the row number is even or odd.
Example. Let
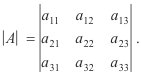
Then the minor of element a21 is
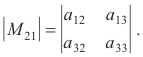
The cofactor of element a21 is
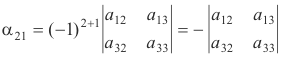
Evaluation of a determinant by minors.
Theorem 1. The value of a determinant of order n is equal to the sum of the products formed by multiplying each element of any selected row (or column) by its cofactor. The value of a determinant of order 1 is the value of the single element of the determinant.
Example. Let
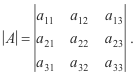
Then
![]()
Where α11, α12, and α13 are the cofactors of a11, a11, and a13.
The usual procedure for evaluating a determinant of order greater than 3 is the following:
Step 1. For some selected row or column use property 7 above to reduce to zero all elements except one.
Step 2. Expand the elements of the selected row (or column) using Theorem 1. This yields a single determinant of lower order than the original determinant.
Step 3. Repeat Step 2 until the remaining determinant is of the second or third order.
Example. Evaluate the determinant

Solution. In general, the first step in the procedure is to locate an element in the matrix that is either 1 or -1. If one doesn’t exist, we create one using property 2 or 7 listed above. In this case there is a -1 in the second column. We will use it to reduce to zero the other elements in the same column. Adding the third row to the first gives
0 0 -2 7
for the new first row.
Adding twice the third row to the second gives
-1 0 4 7
for the new second row.
Subtracting three times the third row from the fourth gives
10 0 -1 -8
for the new fourth row.
We thus have
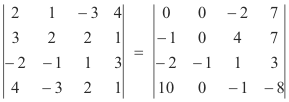
We now expand the determinant along the elements of the second column to obtain
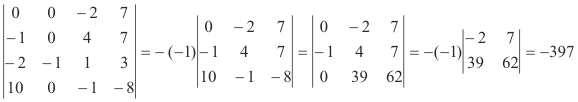
The solution of a system of n linear equations in n unknowns by determinants.
Cramer’s Rule. Given a system of n linear equations in n unknowns
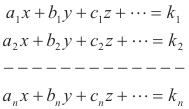
where the n unknowns in the left members are assumed to appear in the same order in all equations and the constant terms, k1, k2, ... , kn, are in the right members. Let D denote the determinant of the coefficients formed from the coefficients in the left members arranged just as they appear in the system. Let Nx be the determinant formed from D by replacing the coefficients of x with the constant terms k1, k2, ... , kn, let Ny be the determinant formed from D by replacing the coefficients of y with the constant terms k1, k2, ... , kn, etc. Then:
Case 1. D ≠ 0. The system has a unique solution given by
x = Nx /D, y = Ny /D, z = Nz /D, ............
Case 2. D = 0 and at least one of Nx , Ny , Nz , ... ≠ 0. The system has no solution. It is inconsistent.
Case 3. D = 0 and Nx , Ny , Nz , ... = 0. The system may or may not have a solution. If it has a solution, the equations are dependent and there will be an infinite number of solutions. If it doesn’t have a solution, the equations are inconsistent.
Linear systems containing fewer equations than unknowns. Ordinarily if there are fewer equations than unknowns in a system, the system will have an infinite number of solutions. However, if the system contains inconsistent equations, there will be no solution.
To solve a consistent system of m equations in n unknowns, where m < n, solve for m of the unknowns in terms of the others.
Linear systems containing more equations than unknowns. Ordinarily if there are more equations than unknowns, the system is inconsistent. However, this need not be the case and the system may contain a number of dependent equations; in which case there may be either one or an infinite number of solutions.
Homogeneous systems. A linear equation is homogeneous if its constant term is zero. Every system of homogeneous equations
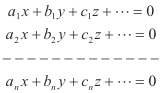
has the so-called trivial solution x = 0, y = 0, z = 0, .....
Theorem. A necessary and sufficient condition that a system of n homogeneous linear equations in n unknowns have solutions other than the trivial solution is that its determinant of the coefficients is zero. If the determinant of the coefficients is zero, it will have an infinite number of solutions.
References
Hawks, Luby, Touton. Second-Year Algebra
Murray R. Spiegel. College Algebra (Schaum)
Raymond W. Brink. A First Year of College Mathematics
Frank Ayres. First Year College Mathematics (Schaum)
James / James. Mathematics Dictionary
Jesus Christ and His Teachings
Way of enlightenment, wisdom, and understanding
America, a corrupt, depraved, shameless country
On integrity and the lack of it
The test of a person's Christianity is what he is
Ninety five percent of the problems that most people have come from personal foolishness
Liberalism, socialism and the modern welfare state
The desire to harm, a motivation for conduct
On Self-sufficient Country Living, Homesteading
Topically Arranged Proverbs, Precepts, Quotations. Common Sayings. Poor Richard's Almanac.
Theory on the Formation of Character
People are like radio tuners --- they pick out and listen to one wavelength and ignore the rest
Cause of Character Traits --- According to Aristotle
We are what we eat --- living under the discipline of a diet
Avoiding problems and trouble in life
Role of habit in formation of character
Personal attributes of the true Christian
What determines a person's character?
Love of God and love of virtue are closely united
Intellectual disparities among people and the power in good habits
Tools of Satan. Tactics and Tricks used by the Devil.
The Natural Way -- The Unnatural Way
Wisdom, Reason and Virtue are closely related
Knowledge is one thing, wisdom is another
My views on Christianity in America
The most important thing in life is understanding
We are all examples --- for good or for bad
Television --- spiritual poison
The Prime Mover that decides "What We Are"
Where do our outlooks, attitudes and values come from?
Sin is serious business. The punishment for it is real. Hell is real.
Self-imposed discipline and regimentation
Achieving happiness in life --- a matter of the right strategies
Self-control, self-restraint, self-discipline basic to so much in life