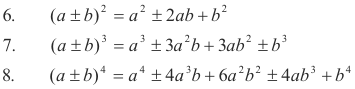
Website owner: James Miller
Special products. Methods for factoring polynomials with integer coefficients. Highest common factor. Relatively prime polynomials. Lowest common multiple.
Special products. The following are some products that occur frequently in mathematics and it is important to be familiar with them.
1. a(c + d) = ac + ad
2. (a + b)(a - b) = a2 - b2
3. (x + a)(x + b) = x2 + (a + b)x + ab
4. (ax + b)(cx + d) = acx2 + (ad + bc)x + bd
5. (a + b)(c + d) = ac + bc + ad + bd
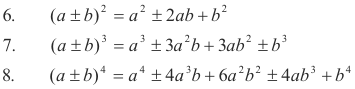
![]()
10. (a + b + c)2 = a2 + b2 + c2 + 2ab + 2ac + 2bc
11. (a + b + c)3 = a3 + b3 + c3 + 3a2(b + c) + 3b2(a + c) + 3c2(a + b) + 6abc
In addition,
a3 - b3 = (a - b)(a2 + ab + b2)
a4 - b4 = (a - b)(a3 + a2b + ab2 + b3)
a5 - b5 = (a - b)(a4 + a3b + a2b2 + ab3 + b4)
a6 - b6 = (a - b)(a5 + a4b + a3b2 + a2b3 + ab4 + b5)
and, in general,
12. an - bn = (a - b)(an-1 + an-2b + an-3b2 + ... + abn-2 + bn-1)
13. an - bn = (a + b)(an-1 - an-2b + an-3b2 - ... + abn-2 - bn-1)
where n is any positive integer (1, 2, 3, 4, ...).
Moreover,
a3 + b3 = (a + b)(a2 - ab + b2)
a5 + b5 = (a + b)(a4 - a3b + a2b2 - ab3 + b4)
a7 + b7 = (a + b)(a6 - a5b + a4b2 - a3b3 + a2b4 - ab5 + b6)
and, in general,
14. an + bn = (a + b)(an-1 - an-2b + an-3b2 - ... - abn-2 + bn-1)
where n is any positive odd integer (1, 3, 5, 7, ...).
Methods for factoring polynomials with integer coefficients
Def. Factor. The factors of a given algebraic expression consist of two or more algebraic expressions which when multiplied together produce the given expression. For example, the algebraic expression x2 + 2xy - 8y2 can be written as the product (x + 4y)(x - 2y).
We shall consider here methods of decomposing a particular type of polynomial, namely one with integer coefficients, into products of polynomials of the same kind i.e. polynomials whose coefficients are also integers. A polynomial which cannot itself be further decomposed into factors whose coefficients are integers is said to be prime. A polynomial is said to be factored completely when it is expressed as a product of prime factors.
The process of factoring a polynomial is a trial and error procedure involving ingenuity and creativity. And there is no guarantee that a given polynomial can be factored. What follows is a list of methods that one should keep in mind when attempting to factor a polynomial. They represent possibilities to be considered. One of them may work.
Possible factoring methods.
1. Common monomial factor.
Type: ac + ad = a(c + d)
Examples.
8x3y + 4x2 = 4x2(2xy + 1)
x3y + 4x2 y - 5x2y3 = x2y(x + 4 - 5y2)
2. Difference of two squares.
Type: a2 - b2 = (a + b)(a - b)
Examples.
4x2 - y2 = (2x + y)(2x - y)
20a2x2 - 45y2 = 5(2ax + 3y)(2ax - 3y)
3. Trinomials that are perfect squares.
Type: a2 + 2ab + b2 = (a + b)2
a2 - 2ab + b2 = (a - b)2
Examples.
x2 + 6x + 9 = (x + 3)2
16x2 - 24xy2 + 9y4 = (4x - 3y2)2
4. Trinomials of the form x2 + qx + r.
Type: x2 + (a + b)x + ab = (x + a)(x + b)
To factor x2 + qx + r, we seek two numbers, a and b, such that ab = r and (a + b) = q. To find a and b, we examine the different pairs of factors of r in order to find a pair whose algebraic sum is q. Another method: Use the Quadratic formula to find the roots of the equation x2 + qx + r = 0.
Examples.
x2 - 5x + 4 = (x - 4)(x - 1) where a = -4, b = -1 so that their sum (a + b) = -5 and their product ab = 4
x2 - 4x - 12 = (x - 6)(x + 2)
5. Trinomials of the form px2 + qx + r.
Type: acx2 + (ad + bc)x + bd = (ax + b)(cx + d)
The easiest way to factor this type is by using the Quadratic formula to find the roots of the equation px2 + qx + r = 0.
Examples.
3x2 - 5x - 2 = (x - 2)(3x + 1) where a = 1, c = 3, b = -2, d =1 found by trial and error
4x2 - 8x -5 = (2x - 5)(2x + 1)
6. Sum or difference of two cubes.
Type: a3 + b3 = (a + b)(a2 - ab + b2)
a3 - b3 = (a - b)(a2 + ab + b2)
Examples.
8x3 + 27y3 = (2x)3 + (3y)3
= (2x + 3y)[(2x)2 - (2x)(3y) + (3y)2]
= (2x + 3y)(4x2 - 6xy + 9y2)
27x3 - 64y3 = (3x - 4y)(9x2 + 12xy + 16y2)
7. Grouping of terms.
Type: ac + bc + ad + bd = c(a + b) + d(a + b) = (a + b)(c + d)
Examples.
2ax - 4by + ay - 2by = 2x(a - 2b) + y(a - 2b) = (a - 2b)(2x + y)
3ax - ay - 3bx + by = a(3x - y) - b(3x - y) = (3x -y)(a - b)
8. Factors of an
![]() bn.
bn.
Type: an - bn = (a - b)(an-1 + an-2b + an-3b2 + ... + abn-2 + bn-1) where n is any positive integer (1, 2, 3, 4, ...).
an + bn = (a + b)(an-1 - an-2b + an-3b2 - ... - abn-2 + bn-1)where n is any positive odd integer (1, 3, 5, 7, ...).
Examples.
64 + y3 = 43 + y3 = (4 + y)(42 - 4y + y2) = (4 + y)(16 - 4y + y2)
x7 -1 = (x - 1)(x6 + x5 + x4 + x3 + x2 + x + 1)
9. Adding and subtracting some perfect square.
Sometimes the addition and subtraction of a perfect square will change a polynomial into a difference of two squares.
Problem. Factor x4 + x2y2 + y4.
Solution. Add and subtract x2y2.
x4 + x2y2 + y4 = x4 + x2y2 + y4 + x2y2 - x2y2
= x4 + 2x2y2 + y4 - x2y2
= (x2 + y2)2 - x2y2
= [(x2 + y2) + xy][(x2 + y2) - xy]
= (x2 + xy + y2)(x2 - xy + y2)
Def. Highest common factor (H. C. F.) of two or more polynomials. The polynomial of highest degree and largest numerical coefficients (apart from trivial changes in sign) which is a factor of all the given polynomials.
Syn. Greatest common divisor
To find the highest common factor of several polynomials first write each polynomial as a product of prime factors. Then note those factors common to all the polynomials and take each common factor to the lowest power to which it occurs in all polynomials.
Problem. Find the H. C. F. of
2233(3x + y)4(x + 1)2, 33x(3x + y)2(x + 1)3, 2332(3x + y)3(x + 1)
Solution. The common factors are 3, (3x + y) and (x + 1). The H. C. F. is 32(3x + y)2(x + 1).
Def. Relatively prime polynomials. Two polynomials are relatively prime if their H. C.
F. is
![]() 1, that is, they have no common factors other than
1, that is, they have no common factors other than
![]() 1.
1.
Def. Lowest common multiple (L. C. M.) of two or more polynomials. The polynomial of lowest degree and smallest numerical coefficients (apart from trivial changes in sign) which contains each of the given polynomials as a factor.
To find the lowest common multiple of several polynomials first write each polynomial as a product of prime factors and then make a list of all the prime factors that occur in the various polynomials. The L. C. M. is the product obtained by multiplying together all of the prime factors in the list, taking each factor to the highest power to which it occurs in any of the given polynomials.
Problem. Find the L. C. M. of
2233(3x + y)4(x + 1)2, 33x(3x + y)2(x + 1)3, 2332(3x + y)3(x + 1)
Solution. The list of factors is 2, 3, x, (3x + y) and (x + 1). The L. C. M. is 2333x(3x + y)4(x + 1)3.
References
Hawks, Luby, Touton. Second-Year Algebra
Murray R. Spiegel. College Algebra
Raymond W. Brink. A First Year of College Mathematics
Jesus Christ and His Teachings
Way of enlightenment, wisdom, and understanding
America, a corrupt, depraved, shameless country
On integrity and the lack of it
The test of a person's Christianity is what he is
Ninety five percent of the problems that most people have come from personal foolishness
Liberalism, socialism and the modern welfare state
The desire to harm, a motivation for conduct
On Self-sufficient Country Living, Homesteading
Topically Arranged Proverbs, Precepts, Quotations. Common Sayings. Poor Richard's Almanac.
Theory on the Formation of Character
People are like radio tuners --- they pick out and listen to one wavelength and ignore the rest
Cause of Character Traits --- According to Aristotle
We are what we eat --- living under the discipline of a diet
Avoiding problems and trouble in life
Role of habit in formation of character
Personal attributes of the true Christian
What determines a person's character?
Love of God and love of virtue are closely united
Intellectual disparities among people and the power in good habits
Tools of Satan. Tactics and Tricks used by the Devil.
The Natural Way -- The Unnatural Way
Wisdom, Reason and Virtue are closely related
Knowledge is one thing, wisdom is another
My views on Christianity in America
The most important thing in life is understanding
We are all examples --- for good or for bad
Television --- spiritual poison
The Prime Mover that decides "What We Are"
Where do our outlooks, attitudes and values come from?
Sin is serious business. The punishment for it is real. Hell is real.
Self-imposed discipline and regimentation
Achieving happiness in life --- a matter of the right strategies
Self-control, self-restraint, self-discipline basic to so much in life