Boundary-value problems of potential theory. Dirichlet and Neumann problems. Poisson�s integral formula for the unit circle and upper half plane.

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

Boundary-value problems of potential theory. Dirichlet and Neumann problems. Poisson’s integral formula for the unit circle and upper half plane.

Boundary-value problems. Many problems in science and engineering when formulated mathematically lead to partial differential equations and associated conditions called boundary conditions. The problem of determining solutions to a partial differential equation which satisfy the boundary conditions is called a boundary-value problem. The boundary conditions, in general, take the form of certain specified requirements for a given set of values of the independent variables (i.e. that set being the boundary points).

Boundary-value problems of potential theory

First boundary-value problem of potential theory (the Dirichlet problem). Let R be some region in space, S be its boundary surface, and f be a function defined and continuous over S. The problem is to find a solution U of the Laplace equation ∇²U = 0 which is regular in R, continuous in R+S and satisfies the equation U = f at the boundary. The solution can be expressed in terms of Green’s function. The problem is encountered in electrostatics and heat flow.

Second boundary-value problem of potential theory (the Neumann problem). Let R be some region in space, S be its boundary surface and f be a function defined and continuous over S and such that

∫∫ fdS

over S vanishes. The problem is to find a solution U of the Laplace equation ∇²U = 0 which is regular in R, which together with its normal derivative (directional derivative of U in the direction of the normal) is continuous in R+S, such that its normal derivative is equal to f on the boundary S. The solution can be expressed in terms of Neumann’s function. The problem is encountered in fluid dynamics. Any two of its solutions differ at most by a constant.

Third boundary-value problem of potential theory (the Robin problem). Let R be some region in space, S be its boundary surface, and k, h, and f be prescribed functions defined and continuous over S. The problem is to find a solution U of the Laplace equation ∇²U = 0 which together with its normal derivative is regular in R, continuous in R+S, and satisfies the equation

k ∂U/∂n + hU = f

on the boundary S. (where ∂U/∂n is the normal derivative of U). This problem includes the other two and is of importance in heat flow and fluid mechanics. If h/k > 0, the problem has at most one solution. The solution can be expressed in terms of Robin’s function.

Def. Normal derivative. The directional derivative of a function in the direction of the normal at the point where the derivative is taken; the rate of change of a function in the direction of the normal to a curve or surface.

James/James. Mathematics Dictionary.

Def. Harmonic function. A function that satisfies Laplace’s equation.

******************************************************

Complex variable methods for solving boundary-value problems involving Laplace’s equation.

Laplace’s equation arises in many branches of physics. It is, for example, satisfied by the electrostatic potential, by the temperature in the case of steady state heat conduction, by the velocity potential in the case of steady, irrotational flow of an ideal fluid, and in other physical situations in which equilibrium conditions prevail.

Hauser. Complex Variables with Physical Applications. p. 268

Complex variable methods can be employed in solving two dimensional versions of the Dirichlet and Neumann problems.

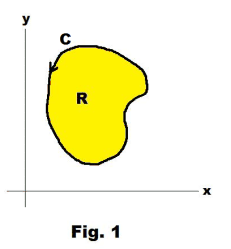
Two dimensional Dirichlet problem. Let R be a simply-connected region bounded by a simple closed curve C as shown in Fig. 1. Find a function Φ(x, y) that satisfies Laplace’s equation in R and takes prescribed values on the boundary C.

Two dimensional Neumann problem. Let R be a simply-connected region bounded by a simple closed curve C. Find a function Φ(x, y) that satisfies Laplace’s equation in R and whose normal derivative ∂Φ/∂n takes prescribed values on the boundary C.

In both of the above problems the region R may be unbounded. For example, R can be the upper half plane with the x axis as the boundary of C.

Solutions to both the Dirichlet and Neumann problems exist and are unique under very mild conditions on the boundary conditions.

A Neumann problem can be stated in terms of a Dirichlet problem. Thus if we can solve the Dirichlet problem we can (at least theoretically) solve the corresponding Neumann problem.

The Dirichlet problem for the unit circle. Poisson’s integral formula. Let C be the unit circle |z| = 1 and let R be its interior. A function which satisfies Laplace’s equation [i.e. is harmonic] at each point (r, θ) in R and takes on the prescribed value F(θ) on C [i.e. Φ(1,θ) = F(θ)], is given by

Proof

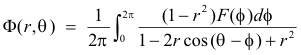
This is Poisson’s integral formula for a circle.

The Dirichlet problem for the half plane. A function which satisfies Laplace’s equation [i.e. is harmonic] in the half plane y > 0 [Im {z} > 0] and which takes on the prescribed value G(x) on the x axis [i.e. Φ(x, 0) = G(x), - < x< ] is given by

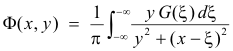
This is Poisson’s integral formula for the half plane.

Procedure for solving Dirichlet and Neumann problems by complex variable methods. The procedure usually used in solving Dirichlet and Neumann problems by complex variable methods consists of three steps:

Step 1. Find a conformal transformation that maps the given region R, along with associated boundary conditions, onto a simpler region for which a solution is known or can be found (such as a unit circle or upper half plane), thus transforming the boundary-value problem for region R into one for the simpler region.

Step 2. Solve the transformed boundary-value problem for the simpler region.

Step 3. Use the inverse mapping to the one used in Step 1 to transform the solution back to the original coordinates to obtain the solution to the given problem.

The Dirichlet and Neumann problems can be solved for any simply-connected region R which can be mapped conformally by an analytic function onto the interior of a unit circle or half plane. Fortunately, it is possible to find transformations which map a large class of regions onto the interior of the unit circle or onto the upper half plane.

Theorem 1. If Φ(x, y) is a harmonic function of x and y in a region R, the function φ(u, v) into which it is transformed by an analytic mapping w = f(z) is a harmonic function of u and v in the image region R'. In other words, a harmonic function is transformed into a harmonic function under a transformation w = f(z) that is analytic.

If the analytic mapping w = f(z) that maps R into R' is given by u = u(x, y), v = v(x, y) and its inverse transformation by x = x(u, v), y = y(u, v), then Φ(x, y) is transformed into φ(u, v) by

Φ(x, y) = Φ[x(u, v), y(u, v)] φ(u, v)

Theorem 1 is a direct consequence of Theorem 2 which follows.

Theorem 2. Let the function Φ(x, y) be transformed into Φ[x(u, v), y(u, v)] by the analytic transformation w = f(z): u = u(x, y), v = v(x, y) with the inverse x = x(u, v), y = y(u, v). Let f '(z) 0. Then

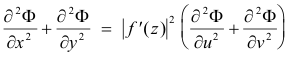
Theorem 3. If Φ = a (a constant) on the boundary or part of the boundary C of a region in the z plane, then φ = a on its image C' in the w plane. Similarly if the normal derivative of Φ is zero, i.e. ∂Φ/∂n = 0 on C, then the normal derivative of φ is zero on C'.

References

Spiegel. Complex Variables. (Schaum)

Hauser. Complex Variables with Physical Applications

James/ James. Mathematics Dictionary

International Dictionary of Applied Mathematics. (D. Van Nostrand)