Website owner:  James Miller

Zeros, poles, Argument principle, Rouche’s theorem

Zeros and poles

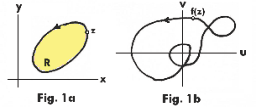
Let f(z) be analytic inside and on a simple closed curve C, except for possibly a finite number of poles in the region R inside C. Consider the curve that is traced out in the w plane by f(z) as the point z goes around C once in the positive direction. As z goes around C, f(z) describes some closed curve. See Fig. 1. How f(z) behaves depends on the number of zeros and poles of f(z) in R.          

Case 1. There are no poles in R. Suppose f(z) has one simple zero in R. Then as z goes around C once in the positive direction, f(z) will wind around the origin once in the positive (counterclockwise) direction. Suppose there are two simple zeros in R. Then as z goes around C once in the positive direction, f(z) will wind around the origin twice in the positive direction. Suppose there is one zero of order three in R. Then as z goes around C once in the positive direction, f(z) will wind around the origin three times in the positive direction.

Case 2. There are no zeros in R. Let f(z) have one simple pole in R. Then as z goes around C once in the positive direction, f(z) will wind around the origin once in the negative (clockwise) direction. If there is one pole of order 3 in R, then as z goes around C, f(z) will wind around the origin three times in the negative direction. If there are 3 simple poles in R, then as z goes around C, f(z) will wind around the origin three times in the negative direction.

Case 3. There are both zeros and poles in R. Suppose f(z) has one simple zero and two simple poles in R. Then as z goes around C once in the positive direction, f(z) will wind around the origin once in the negative direction. Suppose f(z) has three simple zeros and one simple pole in R. Then as z goes around C once in the positive direction, f(z) will wind around the origin twice in the positive direction.

Thus we see that as point z makes one trip around C in the positive direction, f(z) makes n trips around the origin where n is given by the total number of zeros within C minus the total number of poles within C. If n is negative it indicates trips in the negative direction. A zero (or pole) of order m is counted as m zeros (or poles).

How f(z) behaves as z goes around C can also be expressed in terms of the change in the argument of f(z), Δ arg f(z), when z makes one trip about C. If there is a single zero and no poles, Δ arg f(z) = 2π. If there are three zeros and no poles, Δ_C arg f(z) = 3 ·2π = 6π, etc.

Let us now consider an example that will give insight into what is happening. Let f(z) be the polynomial

1)        f(z) = a₀zⁿ + a₁z^n-1 + ... + a_n = a₀(z - z₁)(z - z₂) ... (z - z_n)

which we have decomposed into linear factors. The numbers z₁, z₂, ... , z_n correspond to the zeros of f(z).

From the formula

we know the product of several complex numbers is equal to the sum of the arguments of the factors. Thus

2)        arg f(z) = arg a₀ + arg (z - z₁) + arg (z - z₂) + ........ + arg (z - z_n) .

Let Δ arg f(z) be the change in the argument of f(z) when z makes one trip about C. Then Δ arg f(z) will be equal to 2π times the number of times the point f(z) winds around the origin.     Now it is clear that when z makes one trip about C

3)        Δ arg f(z) = Δ arg a₀ + Δ arg (z - z₁) + Δ arg (z - z₂) + ........ + Δ arg (z - z_n) . 

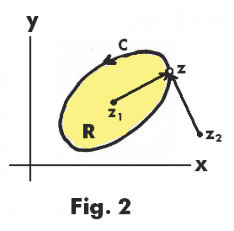
Now Δ arg a₀ = 0 since a₀ is a constant. We note that z - z₁ corresponds to a vector extending from point z₁ to point z. Let us assume that z₁ lies in the interior of the region. See Fig. 2. From the figure it is clear that as the point z goes around the curve C the vector z - z₁ makes a complete revolution about its initial point. Consequently Δ arg (z - z₁) = 2π. Let us now assume that point z₂ lies outside the region as shown in the figure. In this case the vector z - z₂ moves from side to side and returns to its original position without making a revolution about its initial point. Thus Δ arg (z - z₁) = 0. We can reason the same way about all the roots. Thus Δ arg f(z) is equal to 2π times the number of roots of f(z) lying in the interior of the region. And the number of roots inside the region is equal to the number of times the point f(z) winds around the origin.

We just considered a function that had zeros and no poles.   Let us now consider one with poles. Consider the function

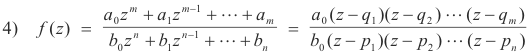
Here q₁, q₂, ... , q_m are the zeros and p₁, p₂, ... , p_n the poles of f(z). Then

5)        arg f(z) = arg a₀ + arg (z - q₁) + arg (z - q₂) + ........ + arg (z - q_n)

                                    - arg b₀ - arg (z - p₁) - arg (z - p₂) - ........ - arg (z - p_n)

When z makes one trip about C, Δ arg f(z) is given by

6)        Δ arg f(z) = Δ arg a₀ + Δ arg (z - q₁) + Δ arg (z - q₂) + ........ + Δ arg (z - q_n)  

                                    - Δ arg b₀ - Δ arg (z - p₁) - Δ arg (z - p₂) - ........ - Δ arg (z - p_n)

We now reason exactly as we did in the previous example.  If the pole p₁ is inside C, then as the point z goes around the curve C the vector z - p₁ makes a complete revolution about its initial point. Consequently Δ arg (z - p₁) = 2π. In 6) this increment has a negative sign attached to it, so it is subtracted from the total for Δ arg f(z). All zeros and poles lying inside the region contribute to the total for Δ arg f(z). Contributions from the zeros are added and contributions from the poles are subtracted. Zeros and poles lying outside the region don’t contribute. Thus Δ arg f(z) is equal to 2π(N - P)   where N is the number of zeros and P is the number of poles inside C. The number of times the point f(z) winds around the origin is given by N - P.                

Theorem 1. If f(z) is analytic inside and on a simple, closed curve C , except for a pole of order p at z = a inside C, then

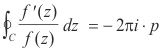
If f(z) is analytic inside and on a simple, closed curve C , except for a zero of order n at z = a inside C, then

Proof

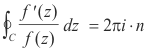
Theorem 2. Let f(z) be analytic inside and on a simple, closed curve C , except for j poles of orders m₁, m₂, ... m_j at points α₁, α₂, ..., α_j and k zeros of orders n₁, n₂, ... n_k at points β₁, β₂, ..., β_k, all located in the region inside C. Suppose that f(z) 0 on C. Then

Proof

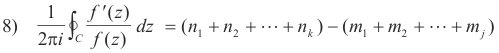
If, in the above theorem, we let P = m₁ + m₂ + ... + m_j and Z = n₁ + n₂ + ... + n_k,

then

Argument principle. Let f(z) be analytic inside and on a simple closed curve C, except for a finite number of poles inside C. Let Z and P be the number of zeros and poles (multiplicities counted, each zero or pole counted a number of times equal to its order) inside C. Let Δ arg f(z) be the change in arg f(z) as z makes one trip about C in the positive (counterclockwise) direction. Then 

            Δ arg f(z) = 2π (Z - P)

Proof

Theorem 3. Let C be a simple, closed curve and R be the open region interior to C. Let f and g be functions analytic on C and its interior R, except for a finite number of zeros and poles in its interior, and satisfying | f | > | g | on C. Then the difference between the number of zeros and poles of f in R (multiplicities counted, each zero or pole counted a number of times equal to its order) is equal to the difference between the number of zeros and poles of f + g in R.

Rouche’s theorem. If f(z) and g(z) are analytic inside and on a simple closed curve C and if |g(z)| < |f(z)| on C, then f(z) + g(z) and f(z) have the same number of zeros inside C.

Proof

References

  Mathematics, Its Content, Method and Meaning. Vol. I

  Wylie. Advanced Engineering Mathematics

  Hauser. Complex Variables with Physical Applications