Sequences, series. Absolute and uniform convergence. Region of convergence. Power series. Taylor�s theorem. Laurent�s theorem. Classification of singular points. Entire, meromorphic functions.

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

Sequences, series. Absolute and uniform convergence. Region of convergence. Power series. Taylor’s theorem. Laurent’s theorem. Classification of singular points. Entire, meromorphic functions.

Sequences of functions. Let {u_n(z)} be a sequence of functions of z

u₁(z), u₂(z), ... ,u_n(z), ...

defined and single-valued in some region of the z plane. Let us denote the limit of the sequence, if a limit exists, by U(z) = .

Theorem. A sequence of functions

u₁(z), u₂(z), ... ,u_n(z), ...

has a limit U(z) as n if, given any number ε we can find a number N (depending in general on both ε and z) such that

| u_n(z) - U(z) | < ε for all n > N

If a sequence has a limit we say it converges. If it does not have a limit we say it diverges.

Region of convergence of a sequence. If a sequence {u_n(z)} converges for all values of z in a region R, we call R the region of convergence of the sequence. A sequence that is not convergent at some value z is called divergent at z.

*****************************

Series of functions

*****************************

Def. Sum of an infinite series. An infinite series of numbers has no sum within the ordinary meaning of the word since no matter how many of the terms one might add, there would always be an unlimited number of them left over. We must therefore define a meaning for the term sum as applied to infinite series.

Consider a series

u₁ + u₂ + u₃ + ... + u_n + ...

and the sequence of partial sums S₁, S₂, S₃, ... where

S₁ = u₁

S₂ = u₁ + u₂

S₃ = u₁ + u₂ + u₃

...............................

S_n = u₁ + u₂ + u₃ + .... + u_n

If S_n, regarded as a function of n, approaches a limit S as n , this limit is called the sum of the infinite series and the series is said to be convergent. If S_n does not approach a limit as n , the series is said to be divergent.

Applying this to our sequence of functions

u₁(z), u₂(z), ... ,u_n(z), ...

we form the series of partial sums {S_n(z)}defined by

S₁(z) = u₁(z)

S₂(z) = u₁(z) + u₂(z)

.................................

S_n(z) = u₁(z) + u₂(z) + ... + u_n(z) .

The infinite series

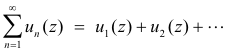
is said to have the sum S(z) if i.e. if the sequence of partial sums {S_n(z)} converges to the limit S(z) as n → ∞.

If the sequence of partial sums {S_n(z)} converges to a limit we say we say the series Σ u_n(z) converges. If it does not converge to a limit we say the series diverges.

Region of convergence of a series. If a series converges for all values of z in a region R, we call R the region of convergence of the series.

Def. Absolute convergence. A series Σu_n(z) is said to converge absolutely (or to be absolutely convergent) if the corresponding positive series Σ | u_n(z) | obtained by replacing all terms of the series by their absolute values converges.

Theorem. The terms of an absolutely convergent series can be arranged in any order and all such rearranged series converge to the same sum. Also the sum, difference and product of absolutely convergent series is absolutely convergent.

Def. Conditional convergence. A series is called conditionally convergent if it is convergent, but not absolutely convergent.

Uniform convergence of a sequence of functions. Let {u_n(z)}, n = 1, 2, 3, ... be an infinite sequence of functions defined on a region R. The sequence is said to converge to U(z), or to have the limit U(z) in R, if for any chosen ε > 0 and each z in R, we can find an N > 0 such that |U(x) - u_n(x)| < ε for all n > N. In such a case we write The number N may depend on z as well as ε. If it depends only on ε and not on z, the sequence is said to converge to U(x) uniformly in R or to be uniformly convergent in R. If a sequence is convergent but not uniformly convergent it is said to be nonuniformly convergent.

Uniform convergence of a series. The infinite series

Σ u_n(z) = u₁(z) + u₂(z) + u₃(z) + ...

is said to be convergent in a region R if the sequence of partial sums {S_n(z)}, n = 1, 2, 3, ... , where S_n(z) = u₁(z) + u₂(z) + ... + u_n(z), is convergent in R. In such as case we write and call S(z) the sum of the series.

It now follows that Σu_n(z) converges to S(z) in R if for any chosen ε > 0 and each z in R we can find an N > 0 such that |S_n(z) - S(z)| < ε for all n < N. If N depends only on ε and not on x, the series is called uniformly convergent in R.

Since S(z) - S_n(z) = R_n(z), the remainder after n terms, we can equivalently say that Σu_n(z) is uniformly convergent in R if for any chosen ε > 0 we can find N depending on ε but not on x such that |R_n(z)| < ε for all z in R. In other words, if a series converges uniformly in a region R, then corresponding to any ε > 0 there exists an integer N such that everywhere in R the sum of the series S(z) can be approximated with an error less than ε by using no more than N terms of the series. This is in sharp contrast to ordinary convergence where, in the neighborhood of certain points in the region of convergence, it may be that no limit can be set on the number of terms required to secure a prescribed degree of accuracy.

Wylie. Advanced Engineering Mathematics. p.572

Theorems on uniform convergence.

Theorem 1. Weierstrass M test. If a sequence of positive constants {M_n} exists such that |u_n(z)| M_n for all values of z in a given region R, and if the series ΣM_n is convergent, then the series Σu_n(z) is uniformly convergent in R.

Theorem 2. Let the series Σu_n(z) be uniformly convergent in a region R and let a function g(z) be bounded in R i.e. |g(z)| < M over R, where M is some constant. Then g(z)Σu_n(z) is uniformly convergent in R. In other words, if the terms of a uniformly convergent series are multiplied by any bounded function of z, the resulting series will also converge uniformly.

Theorem 3. The sum of a uniformly convergent series of continuous functions is a continuous function. In other words, if the series

U(z) = u₁(z) + u₂(z) + ... + u_i(z) + ...

is uniformly convergent and each term u_i(z) is a continuous function of z, then the sum U(z) is a continuous function.

Theorem 4. The integral of the sum of a uniformly convergent series of continuous functions along any curve C lying entirely in the region of uniform convergence can be found by termwise integration of the series. In other words, if the series

U(z) = u₁(z) + u₂(z) + ... + u_i(z) + ...

is uniformly convergent and each term u_i(z) is a continuous function of z, then

where C lies within the region of uniform convergence. Thus, a uniformly convergent series of continuous functions can be integrated term by term.

Theorem 5. If U(z) is the sum of a uniformly convergent series of analytic functions, then the derivative of U(z) at any interior point of the region of uniform convergence can be found by termwise differentiation of the series. In other words, if the series

U(z) = u₁(z) + u₂(z) + ... + u_i(z) + ...

is uniformly convergent and each term u_i(z) is analytic, then this series can be differentiated term by term.

Power series. A series of the form

1) a₀ + a₁z + a₂z² + ... + a_nzⁿ + ... ,

involving positive integral powers of a variable z and constant coefficients a_i is called a power series in z. It is an immediate generalization of the polynomial a₀ + a₁z + a₂z² + ... + a_nzⁿ . A series of the form

2) a₀ + a₁(z - a) + a₂(z - a)² + ... + a_n(z - a)ⁿ + ... ,

is called a power series in z - a.

The power series 2) clearly converges for z = a and this may be the only point for which it converges but it usually converges for other points as well. It can be shown that there is a positive number R such that it converges for |z - a| < R and diverges for |z - a| > R, while for |z - a| = R it may or may not converge. If Γ is a circle of radius R with center at z = a, then the series converges at all points inside Γ and diverges at all points outside Γ, while it may or may not converge on the circle Γ. R is called the radius of convergence and Γ is called the circle of convergence.

Theorems on power series

Theorem 1. A power series converges uniformly and absolutely in any region which lies entirely inside its circle of convergence.

Theorem 2. A power series can be differentiated term by term in any region which lies entirely inside its circle of convergence.

Theorem 3. A power series can be integrated term by term along any curve C which lies entirely inside its circle of convergence.

Theorem 4. The sum of a power series is continuous in any region which lies entirely inside its circle of convergence.

For more information on sequences and series see the following: Sequences and series

Taylor’s theorem. Let f(z) be analytic inside a circle C centered at a and let z be a point inside C. Then

Proof

This is called a Taylor series or Taylor expansion in the neighborhood of point a. The region of convergence is given by |z - a| < R, where the radius of convergence R is the distance from a to the nearest singularity of the function f(z). For |z - a| > R, the series diverges. If the nearest singularity of f(z) is at infinity, the radius of convergence is infinite, i.e. the series converges for all z.

If we set z = a + h, another useful form of Taylor’s Series is obtained:

Often it is necessary to expand functions near points where the function f(z) is not analytic. We may be unable to use a Taylor expansion and must use another expansion called a Laurent’s expansion. The price we pay in using a Laurent’s expansion is that it has terms in both negative as well as positive powers of (z - a) and the coefficients cannot be expressed in terms of evaluated derivatives as with the Taylor expansion.

Laurent’s theorem. Let f(z) be analytic throughout the closed annular region R bounded by two concentric circles, C₁ and C₂, centered at point a and let z be a point in R. Then f(z) can be represented by

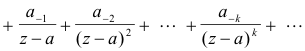
or, equivalently,

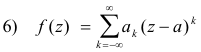
where

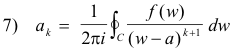
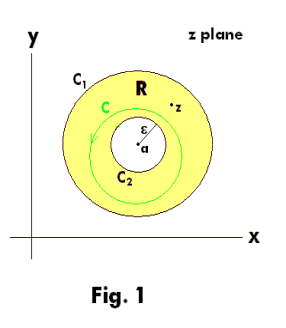
and each integral is taken in the counterclockwise direction around any closed curve C in the annular region that encircles the inner boundary.

Proof

Let the radius of C₂ be ε. Let us note that ε can be allowed to approach zero so that circle C₂ can become infinitely small, approaching point a.

Formula 5) above is called a Laurent series or expansion. The part a₀ + a₁(z - a) + a₂(z - a)² + ... is called the analytic part of the series and the part consisting of inverse powers of (z - a) is called the principal part. If the principal part is zero, the Laurent series reduces to a Taylor series.

Laurent expansions utilized to classify singular points. There are three kinds of isolated singular points:

1. Removable singularity

2. Pole of order n

3. Essential singularity

The Laurent expansion around an isolated singular point can reveal what type of singular point it is.

Theorem 1. Removable singularity. A necessary and sufficient condition for an isolated singular point a of a function f(z) to be a removable singularity is that the principal part of f(z) at z = a vanish i.e. all coefficients a_-1, a_-2, ... be zero.

Theorem 2. Pole of order n. A necessary and sufficient condition for an isolated singular point a of a function f(z) to be a pole of order n is that the principal part of f(z) at z = a contain exactly n terms. In other words, if an isolated singular point a of a function f(z) is a pole of order n the Laurent expansion will have the form

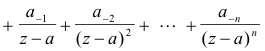
Theorem 3. Essential singularity. A necessary and sufficient condition for an isolated singular point a of a function f(z) to be an essential singularity is that the principal part of f(z) at z = a contain infinitely many non-vanishing coefficients a_-1, a_-2, ... .

Def. Entire function. A function that is analytic everywhere in the finite plane i.e. everywhere except at z = .

Syn. integral function

Examples of entire functions: e^x, sin x, cos x

An entire function can be represented by a Taylor series with an infinite radius of convergence. Conversely, a power series with an infinite radius of convergence represents an entire function.

Def. Meromorphic function. A function that is analytic everywhere in the finite plane except at a finite number of poles.

Example. The function

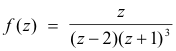
is a meromorphic function. It is analytic everywhere in the finite plane except at poles z = 2 and z = -1

References

Spiegel. Complex Variables (Schaum)

Wylie. Advanced Engineering Mathematics

Hauser. Complex Variables with Physical Applications