Website owner: James Miller
Dot and cross products. Complex conjugate coordinates. Complex differential operators. Gradient, divergence, curl and Laplacian of complex functions.

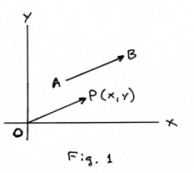
Vector interpretation of complex numbers. A complex number z = x + iy can be viewed as a vector whose initial point is the origin O and whose terminal point P is point (x, y) as shown in Fig. 1. Two vectors having the same length and direction but different initial points, such as OP and AB in Fig. 1, are considered equal. Thus a single complex number can represent any of many vectors — any vector in the plane of the same length and direction — as is the usual case with vectors.
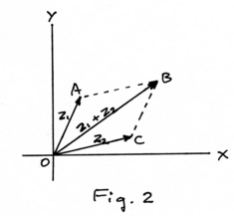
Addition of complex numbers corresponds to the parallelogram law for the addition of vectors. Thus the sum of z1 and z2 corresponds to the diagonal OB of the parallelogram shown in Fig. 2.
Dot product of two complex numbers. The dot product of the two complex numbers z1 = x1 + iy1 and z2 = x2 + iy2 is defined as
1) z1∘z2 = |z1||z2|cos θ = x1x2 + y1y2
![]()
where θ is the angle between z1 and z2 and assumed to be less than 180o.
Syn. scalar product
Cross product of two complex numbers. The cross product of the two complex numbers z1 = x1 + iy1 and z2 = x2 + iy2 is defined as
2) z1×z2 = |z1||z2|sin θ = x1y2 - y1x2
![]()
where θ is the angle between z1 and z2 and assumed to be less than 180o.
From 1) and 2), remembering that ei θ = cos θ + i sin θ, we can easily derive the following theorem:
Theorem.
![]() = z1∘z2 + i(z1×z2) = |z1||z2| ei θ
= z1∘z2 + i(z1×z2) = |z1||z2| ei θ
If z1 and z2 are non-zero, then
1. A necessary and sufficient condition that z1 and z2 be perpendicular is that z1
![]() z2 = 0.
z2 = 0.
2. A necessary and sufficient condition that z1 and z2 be parallel is that z1
![]() z2 = 0.
z2 = 0.
3. The magnitude of the projection of z1 on z2 is |z1
![]() z2|/|z2| .
z2|/|z2| .
4. The area of a parallelogram having sides z1 and z2 is |z1
![]() z2| .
z2| .
Spiegel. Complex Variables. p. 6
Complex conjugate coordinates. The location of points in the complex plane can be
specified by rectangular coordinates (x, y) or polar coordinates (r, θ). We shall now introduce
another set of coordinates by which it is sometimes convenient to identify points in the complex
plane. It is the number pair
![]() where
where
![]() is the conjugate of z. They are called the complex
conjugate coordinates or briefly the conjugate coordinates of the point. The transformation
equations relating the conjugate coordinates with the rectangular coordinates are
is the conjugate of z. They are called the complex
conjugate coordinates or briefly the conjugate coordinates of the point. The transformation
equations relating the conjugate coordinates with the rectangular coordinates are
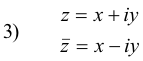
and
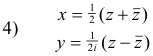
Sometimes, for one reason or another, one may wish to use some non-rectangular coordinates,
such as cylindrical, spherical, curvilinear, etc. on some problem instead of the usual rectangular
coordinates. Another system may be more natural and convenient. We can do this if we wish. It
is only necessary that there exist a one-to-one between the coordinates of the two systems.
Conjugate coordinates represent a kind of curvilinear coordinates. But conjugate coordinates
seem very awkward, obscure and useless. Why would we have any interest in conjugate
coordinates? The answer is they are often very useful in computing things like the gradient,
divergence, curl and Laplacian of a function. To understand why first note that the functions
presented to us are often elementary functions (functions containing algebraic, trigonometric,
logarithmic, etc. terms, functions like 3z2 + sin z + 1) in the complex variable z. To compute
things like the gradient, divergence, curl, etc. we could substitute z = x + iy into the function and
expand, thus changing it into a function in x and y, and then compute the gradient, divergence,
curl, etc. of that function in the usual way. However, that way is tedious and there is an easier
way. We can, in fact, compute the gradient, divergence, curl, etc. directly from the function in
the z form. In fact, the function in z form is already expressed in complex conjugate coordinates!
It is a function in the variable z only but it is actually a function in z and
![]() . It is just that the
. It is just that the
![]() is absent. For insight into this consider a couple of things. First note that any elementary
function in the complex variable z is analytic. Now consider the following theorem:
is absent. For insight into this consider a couple of things. First note that any elementary
function in the complex variable z is analytic. Now consider the following theorem:
Theorem 1. If in any analytic function w = u(x, y) + i v(x, y) the variables x and y are
replaced by their equivalents in terms of z and
![]() , namely,
, namely,
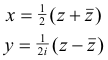
w will appear as a function of z alone.
If we were given a function in the variable z and substituted z = x + iy into it to change it to a function in x and y and then substituted
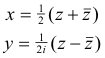
into it, the new expression would initially contain the variable
![]() , but the
, but the
![]() would fall out and
we would get back our original expression in the variable z alone. And Theorem 1 tells us why
the
would fall out and
we would get back our original expression in the variable z alone. And Theorem 1 tells us why
the
![]() falls out. The expression is analytic.
falls out. The expression is analytic.
Complex differential operators. We define the differential operators ∇ (del) and
![]() (del
bar) as follows:
(del
bar) as follows:
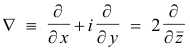
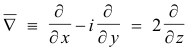
Derivation for conjugate coordinates
Gradient, divergence, curl and Laplacian
We will use the operator ∇ to define the gradient, divergence, curl and Laplacian of various functions. In the discussion we will use the following notation:
● F(x, y) represents a real continuously differentiable function of x and y (a scalar)
● A(x, y) = P(x, y) + i Q(x, y) represents a complex continuously differentiable function of x and y (a vector)
● G(z,
![]() ) represents the function obtained by substituting
) represents the function obtained by substituting
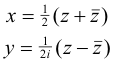
in F(x, y).
● B(z,
![]() ) represents the function obtained by substituting
) represents the function obtained by substituting
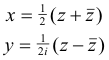
in A(x, y).
Gradient of a real function. We define the gradient of a real function F (scalar) by
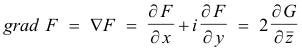
Geometrically, this represents a vector normal to the curve F(x, y) = c where c is a constant.
Gradient of a complex function. We define the gradient of a complex function A = P + iQ (vector) by
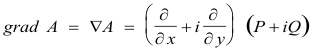
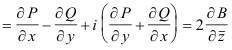
We note that if B is an analytic function of z, then
![]() . Thus the gradient is zero, i.e.
. Thus the gradient is zero, i.e.
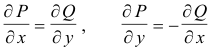
showing the Cauchy-Riemann equations are satisfied in this case.
Divergence of a complex function. By using the dot product of two complex numbers as extended to operators, we define the divergence of a complex function (vector) by
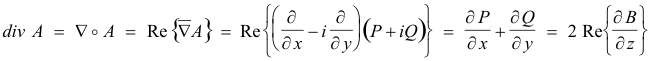
The divergence is always a real function.
Curl of a complex function. By using the cross product of two complex numbers as extended to operators, we define the curl of a complex function (vector) by
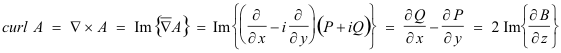
Laplacian. The Laplacian operator is defined as the dot product of ∇ with itself i.e.
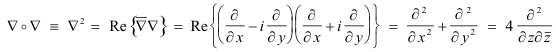
Example. Let B = 3z2 + 4
![]() . Find grad B, div B, curl B, Laplacian B.
. Find grad B, div B, curl B, Laplacian B.
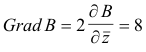
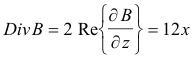
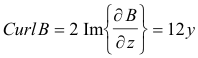
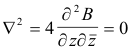
Some identities involving the gradient, divergence and curl. The following identities hold if A1, A2 and A3 are differentiable functions.
1. grad (A1 + A2) = grad A1 + grad A2
2. div (A1 + A2) = div A1 + div A2
3. curl (A1 + A2) = curl A1 + curl A2
4. grad (A1A2) = (A1)( grad A2) + (grad A1)(A2)
5. curl grad A = 0 if A is real or, more generally, if Im{A} is harmonic
5. div grad A = 0 if A is imaginary or, more generally, if Re{A} is harmonic
Spiegel. Complex Variables (Schaum). p. 69 -70
References
Mathematics, Its Content, Methods and Meaning
James and James. Mathematics Dictionary
Spiegel. Complex Variables (Schaum)
Wylie. Advanced Engineering Mathematics
Jesus Christ and His Teachings
Way of enlightenment, wisdom, and understanding
America, a corrupt, depraved, shameless country
On integrity and the lack of it
The test of a person's Christianity is what he is
Ninety five percent of the problems that most people have come from personal foolishness
Liberalism, socialism and the modern welfare state
The desire to harm, a motivation for conduct
On Self-sufficient Country Living, Homesteading
Topically Arranged Proverbs, Precepts, Quotations. Common Sayings. Poor Richard's Almanac.
Theory on the Formation of Character
People are like radio tuners --- they pick out and listen to one wavelength and ignore the rest
Cause of Character Traits --- According to Aristotle
We are what we eat --- living under the discipline of a diet
Avoiding problems and trouble in life
Role of habit in formation of character
Personal attributes of the true Christian
What determines a person's character?
Love of God and love of virtue are closely united
Intellectual disparities among people and the power in good habits
Tools of Satan. Tactics and Tricks used by the Devil.
The Natural Way -- The Unnatural Way
Wisdom, Reason and Virtue are closely related
Knowledge is one thing, wisdom is another
My views on Christianity in America
The most important thing in life is understanding
We are all examples --- for good or for bad
Television --- spiritual poison
The Prime Mover that decides "What We Are"
Where do our outlooks, attitudes and values come from?
Sin is serious business. The punishment for it is real. Hell is real.
Self-imposed discipline and regimentation
Achieving happiness in life --- a matter of the right strategies
Self-control, self-restraint, self-discipline basic to so much in life