Website owner: James Miller
Calculus of variations. Functionals. Euler’s equation. Beltrami Identity. Brachistochone problem. Minimal surface of revolution. Isoperimetric problems.
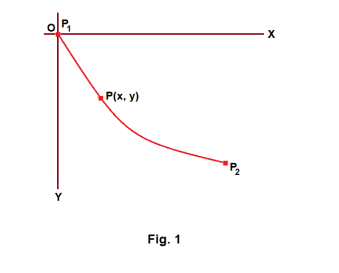
Time required for a marble to descend to the bottom of a chute. A marble starts from rest at point P1 at the top of a chute and rolls (or slides) frictionlessly down the chute to point P2 at the bottom. How long does it take the marble to go from P1 to P2?
Construct the coordinate system shown in Fig. 1 with the origin O at point P1, the x axis horizontal, and the y axis pointed downward. The point P1 is then at coordinates (0, 0). Assume point P2 has coordinates (x2, y2). In addition, assume that the path of the chute is given by the function

1) y = f(x), 0 ≤ x ≤ x2
where f is a continuously differentiable function. Then the time required for the marble to descend to the bottom of the chute is given by
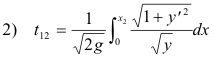
where g is the acceleration of gravity and yʹ = dy/dx.
Examples of problems studied in the Calculus of Variations. The following are examples of the kind of problems studied in the calculus of variations:
1. The curve of fastest descent. Question. Given a chute following curve X from a point P1 at the top to a point P2 at the bottom. Of all possible curves connecting points P1 and P2, for which curve will a marble running down the curve arrive at point P2 the fastest i.e which curve is the curve of fastest descent? Answer: A cycloid passing through the two points (called a brachistochrone). This question of the curve of fastest descent for a marble rolling down a chute is a question posed by the mathematician John Bernoulli in 1696 and is known as the brachistochone problem. It is one of the first problems posed whose solution required the ideas of the calculus of variations. Finding the solution to the brachistochone problem involves solving the following minimal problem: Among all possible functions
y = f(x), 0 ≤ x ≤ x2
subject to conditions
f(0) = 0, f(x2) = y2 ,
find that one which corresponds to the least value of
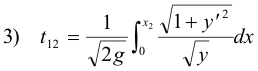
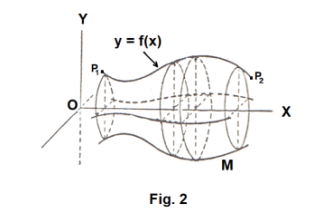
Def. Surface of revolution. A surface in three dimensional space generated by revolving a plane curve about an axis in its plane. In Fig. 2 the surface M is generated by revolving about the x axis the curve segment y = f(x) joining P1 - P2 .
2. The surface of revolution of least area. Question. Among all possible curves joining two points of a plane, which curve when rotated around the x axis, generates the surface of least area?
Let us denote the given points by P1 (x1, y1) and P2 (x2, y2) and consider an arbitrary curve given by the equation
4) y = f(x)
joining the points. The function f will satisfy the condition
5) f(x1) = y1 , f(x2) = y2 .
When rotated around the x axis this curve describes a surface with an area numerically equal to the value of the integral
![]()
The value of S will depend on the choice of the function f(x). Among all functions f(x) satisfying 5) we wish to find that function that gives the least value to the integral 6).
The simplest type integral treated by methods of the Calculus of Variations. Note that the integrals of equations 3) and 6) are both of the general type
![]()
This is the simplest type integral treated by the Calculus of Variations.
The concept of the functional. Let Q be a set of objects of any kind. The objects might be numbers, points of a space, curves, surfaces, functions, states of a mechanical system, motions of a mechanical system, etc. The nature of the objects is immaterial. If to every element x of the set Q there corresponds a number y, we say there is defined on the set Q a functional y = F(x).
The problem of the Calculus of Variations may be stated as follows: Among all elements x of a set Q, find that element for which the functional y = F(x) has the smallest value.
Every functional is defined by two factors: the set Q of elements on which it is given and the law by which every element corresponds to a number.
Calculus of variations. The study of the theory of maxima and minima of definite integrals whose integrand is a known function of one or more independent variables and one or more dependent variables and their derivatives, the problem being to determine the dependent variables so the integral will be a maximum or a minimum. The simplest such integral is of the form
![]()
where y(x) is to be determined to make I a maximum or minimum (whichever is desired). The name calculus of variations originated as a result of notations introduced by Lagrange in about 1760. Other integrals studied are of the form
![]()
where y1, ... , yn are unknown functions of x and y, or multiple integrals such as
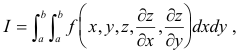
where z is an unknown function of x and y, or multiple integrals of higher order or of various numbers of independent variables (the integrand may also be a function of derivatives of higher order than the first). James and James. Mathematics Dictionary
Euler’s equation (Calculus of Variations). The differential equation
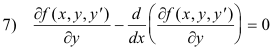
where
![]()
A necessary condition that y(x) minimize the integral
![]()
is that y(x) satisfy Euler’s equation. This condition, and the more general necessary condition,
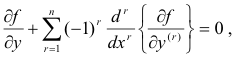
where
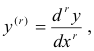
for y(x) to minimize the integral
![]()
were first discovered by Euler in 1744. For the double integral
![]()
Euler’s equation becomes
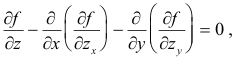
where
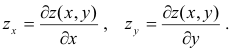
James and James. Mathematics Dictionary
Derivation of Euler’s equation
Another form of the Euler Equation. Let us use a different nomenclature. If we use F(x, y, yʹ) instead of f(x, y, yʹ) and use subscript notation for derivatives, then
8) F(x, y, yʹ) = f(x, y, yʹ)
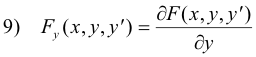
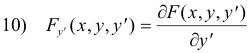
and Euler’s equation 7) becomes
![]()
If now we take the derivative indicated in the second term using the general formula
![]()
we find that that second term becomes
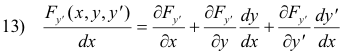
or, more compactly,
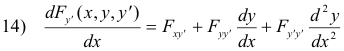
or even more compactly,
![]()
Thus Euler’s equation 7) becomes
16) Fy(x, y, yʹ) - Fxyʹ(x, y, yʹ) - Fyyʹ(x, y, yʹ)yʹ - Fyʹyʹ(x, y, yʹ)yʹʹ = 0
or, more concisely,
![]()
Analogy with a problem in differential calculus. The problem of finding
that function y(x) that minimizes the integral
![]()
is analogous to a situation in differential calculus. In differential calculus the stationary points of the function y = f(x) correspond to those points at which df(x)/dx = 0. The maxima and minima of y = f(x) will be found among the stationary points and we have to perform tests to determine if a particular stationary point is a maximum point, minimum point, or neither. In the same way, Euler’s equation provides us with a list of stationary points and one must perform tests to determine if a particular stationary point is a maximum point, minimum point, or neither. Just as df(x)/dx = 0 represents a necessary condition for a maximum or minimum of the function y = f(x), so satisfaction of Euler’s equation is a necessary condition for the function y(x) to be a maximum or minimum of the integral ∫(x, y, yʹ)dx.
Def. Extremal. A curve corresponding to any solution of Euler’s Equation.
Formula for Euler’s Equation when the integrand does not explicitly contain x. If the integrand F(x, y, yʹ) does not contain x explicitly an equation called the Beltrami identity can be used. It is
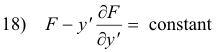
For this situation it is the equivalent of Euler’s equation and greatly reduces the work involved.
Derivation of the Beltrami Identity
Solution to the problem of the curve of fastest descent (brachistochone problem). Finding the curve of fastest descent reduces to the problem of finding that function y = y(x) that minimizes the integral
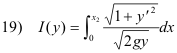
subject to boundary conditions y(0) = 0 , y(x2)= y2.
Here
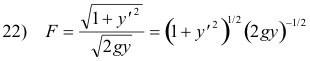
For most problems one would use the Euler Equation
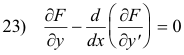
however, in this case, since the variable x does not appear explicitly in the function F, we can use the Beltrami identity
![]()
Let us compute ∂F/∂yʹ:
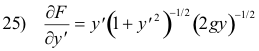
So
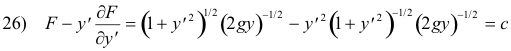
which reduces to
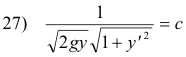
Squaring and rearranging gives
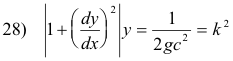
where k is a new (positive) constant. This reduces to
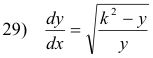
The solution to this equation is
![]()
which are the equations of a cycloid.
Solution to the problem of finding the surface of revolution of least area. Finding the surface of revolution of least area reduces to the problem of finding that function y = y(x) that minimizes the integral
![]()
subject to boundary conditions y(x1) = y1 , y(x2) = y2 .
Here
![]()
Here again, since the variable x does not appear explicitly in the function F, we can use the Beltrami identity
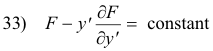
Let us compute ∂F/∂yʹ:
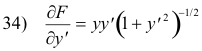
So
![]()
which reduces to
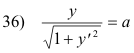
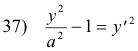
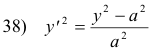
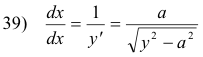
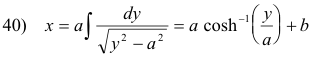
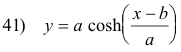
which is the equation of a catenary. In terms of e,
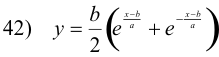
Euler’s equation for integrals involving several functions. The simplest integral in the Calculus of Variations
![]()
involves a single function y = f(x). In applications these integrals arise in cases involving only a single functional dependence. An example of a single functional dependence is a curve in the plane defined by y = f(x). One, however, does often encounters problems involving multiple functional dependencies. An example involving two functional dependencies can be found in a curve in three dimensional space where we need to use two functions, y = y(x) and z = z(x), to define it. An example involving three functional dependencies is the motion of a point in space as a function of time. It can be described by the use of three functions, x = x(t), y = y(t), z = z(t).
Let us consider a problem involving an integral that depends on two functions y = y(x) and z = z(x):
![]()
These two functions,
45) y = y(x), z = z(x),
can be viewed as defining a curve in three-dimensional x-y-z space.
Assume that the admissible pairs of functions y(x) and z(x) are defined by the conditions:
1. The functions y = y(x), z = z(x) are continuously differentiable on the segment [x1, x2].
2. At the ends of the segment these functions have given values
y(x1) = y1, y(x2) = y2
z(x1) = z1, z(x2) = z2 .
In three-dimensional x-y-z space each pair of admissible functions will correspond to a curve p passing through the points
M1(x1, y1, z1),M2(x2, y2, z2) .
We wish to find the minimum of the integral 44) on the set of all such p curves.
The analysis is essentially the same as the analysis for the case of the simplest integral with a single function as discussed under Derivation of Euler’s equation. Let y(x) and z(x) be the functions we seek i.e. the functions that minimize integral 44). Let η(x) and ζ(x) be any continuously differentiable functions vanishing at the ends of the segment [x1, x2]. Then y* = y + αη(x) and z* = z + αζ(x) represent families of functions neighboring y(x) and z(x). Substituting x* and y* into the integral 44) gives
![]()
This function can be regarded as a function of α alone with a minimum at α = 0 i.e.
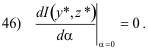
Using Leibniz’s Rule for differentiating an integral with respect to a parameter under an integral sign, we compute the derivative of 45) with respect to α as
![]()
![]()
For the situation where α = 0 we have
![]()
We now transform this equation by integration by parts to obtain
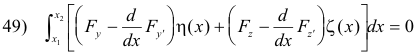
This equation must be satisfied for any two continuously differentiable functions η(x) and ζ(x) vanishing at the ends of the interval. The only way this can occur is that
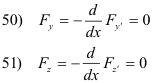
Theorem 1. A necessary condition for the functions y(x) and z(x) to minimize the integral
![]()
is
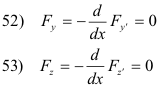
For the general case of an integral containing n functions, there will be n equations that need to be satisfied.
The minimum problem for a multiple integral. Consider the integral
![]()
(where ux = ∂u/∂x and uy = ∂u/∂y). We wish to find that function u(x, y), subject to the following constraints, that makes the value of the integral I(u) a minimum.
Let R be a region in the xy plane bounded by the contour C. The set of admissible functions is defined by the conditions:
1. u(x, y) is continuously differentiable on the region R
2. On C the function u takes on the given values
u|C = f(M)
The given boundary values for u(x, y) determine a space curve Γ above C in x-y-u space where each point on Γ has coordinates [x, y, u(x,y)]. Considering all possible surfaces S passing through Γ and lying above R, we want to find that particular surface for which I(u) is minimal.
Let u(x, y) be that function that minimizes integral 54). Let η(x, y) be any continuously differentiable function vanishing on C. Then u* = u + αη(x, y) represents a family of functions neighboring u(x,y). Substituting x* and y* into the integral 54) gives
![]()
This function can be regarded as a function of α alone with a minimum at α = 0 i.e.
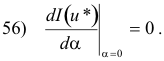
Using Leibniz’s Rule for differentiating an integral with respect to a parameter under an integral sign, we compute the derivative of 55) with respect to α as
![]()
For the situation where α = 0 we have
![]()
Now the following equation is an identity (as can be shown by expanding the right side)
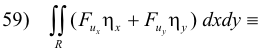
![]()
Applying the Divergence Theorem (two dimensional version) to the first term on the right side, we obtain
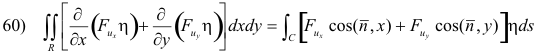
where the right side of this equation is a contour integral around curve C bordering region R. Now on curve C the function η is equal to zero, so the contour integral equals zero, and equation 60) becomes
![]()
The first term on the right side of equation 59) is then zero and equation 59) becomes
![]()
Substituting 62) into 58) gives
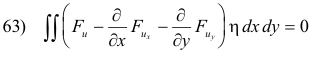
This equation must be satisfied for every function η which is continuously differentiable and vanishes on the boundary C. We can conclude then that the equation
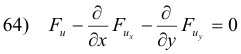
must be satisfied at all points of the region R. So if the function u represents a minimum it must satisfy this equation.
Theorem 2. A necessary condition for a function u(x, y) to be a minimal surface of the integral
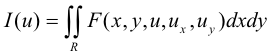
is
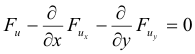
Isoperimetric problems.
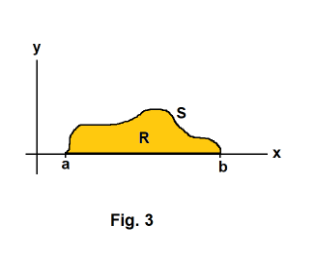
Problem 1. Let a and b be two points on the x axis joined by the chord ab and a string S of length l as shown in Fig. 3. What shape must the string take to make the area of the region R between the string and chord a maximum? Represent the string by the function y = y(x). The area under y = y(x) is given by
![]()
and the length of the string is given by
![]()
What function y(x) will make the area of R a maximum? This is an example of a general class of problems that lend themselves to the methods of the calculus of variations. They are called isoperimetric problems and are problems where one wishes to make one integral a maximum or minimum while keeping constant the integral of a second given function.
Let F(x, y, yʹ) and φ(x, y, yʹ) be two functions which, together with their derivatives of the first two orders, are continuous in some region R of the x-y plane. Let
![]()
where the curve y = y(x) lies in R. Problem: To find that function y = y(x) that makes I(y) = ∫F(x, y, yʹ)dx a minimum (or a maximum) subject to the constraint that ∫φ(x, y, yʹ)dx maintains the fixed value of K.
Theorem 3. A necessary condition that the function y = y(x) makes
I (y) = ∫F(x, y, yʹ)dx a minimum (or a maximum) while ∫φ(x, y, yʹ)dx has the fixed value of K is
![]()
This is the parametric case of Euler’s equation. It expresses a necessary condition for a minimum (or maximum) in terms of an unknown constant, λ. The extremals depend on λ and on the two other constants of integration.
Going back now to problem 1 above we have
![]()
![]()
Euler’s equation then becomes:
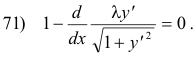
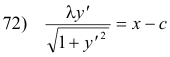
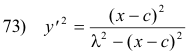
Thus
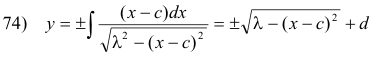
or
75) (x - c)2 + (y - d)2 = λ2
The extremal is thus the arc of a circle joining the two points and having the prescribed length.
References
Osgood. Advanced Calculus.
James and James. Mathematics Dictionary.
Mathematics, Its Content, Methods and Meaning. Vol. II
Jesus Christ and His Teachings
Way of enlightenment, wisdom, and understanding
America, a corrupt, depraved, shameless country
On integrity and the lack of it
The test of a person's Christianity is what he is
Ninety five percent of the problems that most people have come from personal foolishness
Liberalism, socialism and the modern welfare state
The desire to harm, a motivation for conduct
On Self-sufficient Country Living, Homesteading
Topically Arranged Proverbs, Precepts, Quotations. Common Sayings. Poor Richard's Almanac.
Theory on the Formation of Character
People are like radio tuners --- they pick out and listen to one wavelength and ignore the rest
Cause of Character Traits --- According to Aristotle
We are what we eat --- living under the discipline of a diet
Avoiding problems and trouble in life
Role of habit in formation of character
Personal attributes of the true Christian
What determines a person's character?
Love of God and love of virtue are closely united
Intellectual disparities among people and the power in good habits
Tools of Satan. Tactics and Tricks used by the Devil.
The Natural Way -- The Unnatural Way
Wisdom, Reason and Virtue are closely related
Knowledge is one thing, wisdom is another
My views on Christianity in America
The most important thing in life is understanding
We are all examples --- for good or for bad
Television --- spiritual poison
The Prime Mover that decides "What We Are"
Where do our outlooks, attitudes and values come from?
Sin is serious business. The punishment for it is real. Hell is real.
Self-imposed discipline and regimentation
Achieving happiness in life --- a matter of the right strategies
Self-control, self-restraint, self-discipline basic to so much in life