Tensors, contravariant and covariant components of a vector in a curvinilinear coordinate system, notations and abbreviations

SolitaryRoad.com

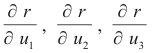
Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

TENSORS, CONTRAVARIANT AND COVARIANT COMPONENTS OF A VECTOR IN A CURVINILINEAR COORDINATE SYSTEM, NOTATIONS AND ABBREVIATIONS

Contravariant and covariant components of a vector in a curvinilinear coordinate system. Suppose we are given a system of equations

u₁ = u₁(x, y, z)

u₂ = u₂(x, y, z)

u₃ = u₃(x, y, z)

and, the inverse transformation

x = x(u₁, u₂, u₃)

y = y(u₁, u₂, u₃)

z = z(u₁, u₂, u₃)

defining a curvilinear coordinate system in space in some region R.

Contravariant components. Consider a coordinate system with its origin located at a point P in region R and with unitary base vectors

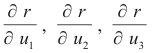
where r is the position vector of P given by

r = x(u₁, u₂, u₃) i + y(u₁, u₂, u₃) j + z(u₁, u₂, u₃) k .

Then any vector A can be expressed with respect to this coordinate system in terms of its base vectors as

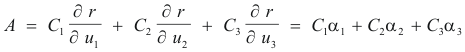
where C₁, C₂, C₃ are called the contravariant components of A.

Covariant components. Consider a coordinate system with its origin located at a point P in region R and with unitary base vectors

Then any vector A can be expressed with respect to this coordinate system in terms of its base vectors as

where c₁, c₂, c₃ are called the covariant components of A.

Question. Let A be a given vector defined with respect to two general curvilinear coordinate systems and . 1. What is the relationship between the contravariant components of A in the two systems? 2. What is the relationship between the covariant components of A in the two systems?

Answer. We answer the two questions:

1. Contravariant components. Let vector A’s contravariant components with respect to system be and its contravariant components with respect to system be Then

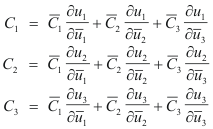
or more briefly

Proof.

Due to symmetry, by interchanging the roles of the and , we see that

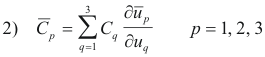
These results lead us to adopt the following definition: If three quantities of a coordinate system are related to three other quantities of another coordinate system by the transformation equations 1) or 2), then the quantities are called components of a contravariant vector or a contravariant tensor of the first rank.

2. Covariant components. Let vector A’s covariant components with respect to system be and its covariant components with respect to system be Then

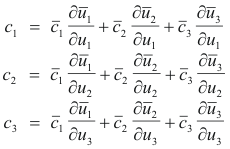
or more briefly

Proof.

Due to symmetry, by interchanging the roles of the and , we see that

These results lead us to adopt the following definition: If three quantities of a coordinate system are related to three other quantities of another coordinate system by the transformation equations 3) or 4), then the quantities are called components of a covariant vector or a covariant tensor of the first rank.

In generalizing these concepts to higher dimensions and in generalizing the concept of vector we are lead to tensor analysis.

Notations and abbreviations of tensor analysis

Notations for variables. In tensor analysis we use both superscripts and subscripts in denoting variables. We may refer to a set of variables x¹, x², ..., xⁿ or to the set of variables x₁, x₂, ..., x_n .

Notations for coordinate transformations. Let and be the coordinates of a point with respect to two different frames of reference and suppose a transformation of coordinates is defined between the two frames of reference by the system

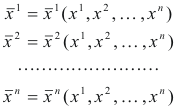
This system can be denoted by the shorthand notation

There will then be an inverse transformation given by

The summation convention. The summation convention is the convention of letting the repetition of an index (subscript or superscript) in a given term denote a summation with respect to that index over its range. For example, the sum

a₁x¹ + a₂x² + ... + a_nx⁶

is denoted by the shorthand notation a_ixⁱ. Instead of using the index i in this example we could have used another letter, say q, and the sum could be written a_qx^q. A repeated index, such as i in a_ixⁱ, is called a dummy index of umbral index.

Free index. An index that occurs only once in a given term is called a free index. A free index stands for any of the numbers 1, 2, ... , n. An example is k in the equations 5) and 6) above.

Contravariant tensor of the first rank (or first order). If n quantities in a coordinate system are related to n other quantities in another coordinate system by the transformation equations

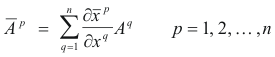
or, by the conventions and abbreviations we have adopted,

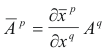
they are called components of a covariant tensor of the first rank (or first order). [they may also be called components of a contravariant vector]

Covariant tensor of the first rank (or first order). If n quantities in a coordinate system are related to n other quantities in another coordinate system by the transformation equations

or, by our conventions,

they are called components of a covariant tensor of the first rank (or first order). [they may also be called components of a covariant vector]

Subscript and superscript conventions. Superscripts are used to indicate contravariant components. Subscripts are used to indicate covariant components. Either subscripts or superscripts can be used for coordinates.

Note. Instead of speaking of a tensor whose components are A^p or A_p we often refer simply to the tensor A^p or A_p.

Contravariant tensor of the second rank. If n² quantities in a coordinate system are related to n² other quantities in another coordinate system by the transformation equations

or, by our conventions,

they are called components of a contravariant tensor of the second rank (or of rank two).

Note. The tensors and are two dimensional arrays containing n rows and n columns. The integers p, r and q, s are row and column indices pointing to elements within the arrays. We can speak of a tensor (tensor array) or we can speak of an element within the tensor, say or . Thus we use the same notation for both the tensor and elements within the tensor, a possible cause for confusion. These arrays represent a generalization of the concept of a vector leading into tensor analysis.

Covariant tensor of the second rank. If n² quantities in a coordinate system are related to n² other quantities in another coordinate system by the transformation equations

or, by our conventions,

they are called components of a covariant tensor of the second rank.

Mixed tensor of the second rank. If n² quantities in a coordinate system are related to n² other quantities in another coordinate system by the transformation equations

or, by our conventions,

they are called components of a mixed tensor of the second rank.

Tensors of rank greater than two. Tensors of rank greater than two are easily defined. For example, the tensor , a mixed tensor of rank 5, contravariant of order 3 and covariant of order 2, is defined by the following relation

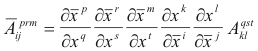
Note the pattern of the indices in the successive fractions

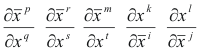
Each index of is paired with its counterpart in i.e. p is paired with q, r is paired with s, m is paired with t, etc. The order of the fractions is the same as the order of the indices in i.e. p, r, m, i, j. The covariant fractions are the same as the contravariant fractions, but inverted.

References.

Spiegel. Vector Analysis. Chap. 7, 8.