Differentiation, implicit differentiation, derivatives of higher order, critical points, inflection points, maxima and minima

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

DIFFERENTIATION, IMPLICIT DIFFERENTIATION, DERIVATIVES OF HIGHER ORDER, INFLECTION POINTS, CRITICAL POINTS, MAXIMA AND MINIMA

The process of differentiation involves applying the various differentiation rules and formulas (the main ones having been memorized) to the function for which we want the derivative.

Differentiation examples.

Problem 1. Find the derivative of y = 8x⁴ + 5x² - 9x

Solution.

= 8(4x³) + 5(2x) - 9(1) (by Rule 10)

= 32x³ + 10x - 9

Problem 2. Find the derivative of y = sin 3x + cos 2x.

Solution.

= 3 cos 3x - 2 sin 2x

Problem 3. Find the derivative of

Solution.

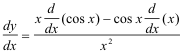
Problem 4. Find the derivative of e^-xln x.

Solution.

Implicit differentiation. An equation of the form y = f(x) is said to define y as an explicit function of x. When y is given as an explicit function of x there is no difficulty in obtaining dy/dx using our rules and formulas for differentiating functions. If, however, y is given as an implicit function of x through an equation of the form f(x, y) = 0 it may be inconvenient or impossible to solve the equation for y in terms of x. There is, nonetheless, a method of finding dy/dx without solving the equation for y. The method is called implicit differentiation. In general, for implicit functions, the method of implicit differentiation is the most convenient and practical method to use for differentiating.

The method consists in 1. Differentiating the equation as it stands with respect to x, regarding y as an unknown function of x having a derivative dy/dx, and 2. Solving the resulting equation for dy/dx. We illustrate with an example.

Problem. Given equation

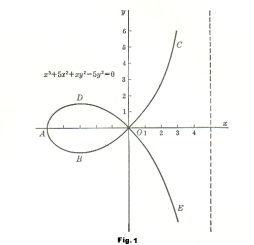
1) x³ + 5x² + xy² - 5y² = 0.

Find dy/dx.

Solution.

Step 1. Differentiate each term of the equation with respect to x regarding, y as an unknown function of x:

Step 2. Regard dy/dx as the unknown and solve the equation by the usual methods.

A graph of equation 1) is shown in Fig. 1. At any point that we choose on the locus of the equation the value of dy/dx will be given by 2).

Derivatives of Higher Order. The derivative dy/dx of a function y = f(x) is itself a function of x. Thus its derivative can be found in turn. It is called the second derivative of the function. Similarly the derivative of the second derivative is called the third derivative, and so on for still higher derivatives.

Notations for higher order derivatives.

Second derivative:

Third derivative:

N-th derivative:

Note. The derivative of a given order at a point can exist only when the function and all derivatives of lower order are differentiable at the point.

Example.

Successive differentiation of implicit functions. Suppose y is defined implicitly as a function of x in an equation of the form f(x, y) = 0 where y cannot be solved for x and one wishes to compute higher order derivatives of y with respect to x. We can do so using the method of implicit differentiation. The following example illustrates the technique.

Problem. Given the equation x² - y² = a². Find

Solution.

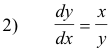
Now take the derivative of 2):

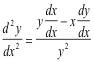
Substituting in the value of dy/dx = x/y from 2) we get

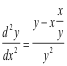
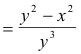
All admissible values of x and y must satisfy the original equation x² - y² = a². Consequently we can replace y² - x² by -a² and write the result in the simpler form

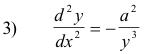
Taking the third derivative with respect to x we get

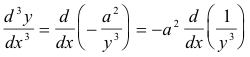
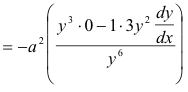
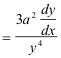
Then using the fact that dy/dx = x/y, we get

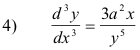
Signs of the first and second derivatives. We now consider the meanings of positive and negative values for dy/dx and d²y/dx².

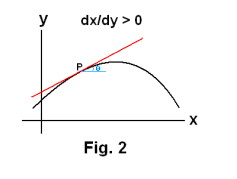
dy/dx is positive. The curve rises with increasing x. The tangent line has a positive slope. See Fig. 2. The inclination angle θ is positive.

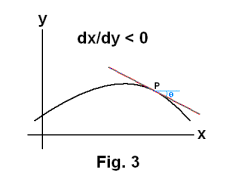
dy/dx is negative. The curve drops with increasing x. The tangent line has a negative slope. See Fig. 3. The inclination angle θ is negative.

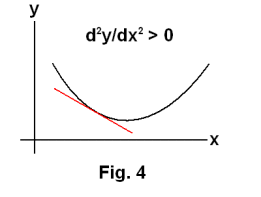
d²y/dx² is positive. The slope is increasing as x increases. The tangent line turns in a counterclockwise manner as it traverses the curve from left to right. The arc is concave upwards. The tangent line lies below the curve. See Fig. 4.

d²y/dx² is negative. The slope is decreasing as x increases. The tangent line turns in a clockwise manner as it traverses the curve from left to right. The arc is concave downwards. The tangent line lies above the curve. See Fig. 5.

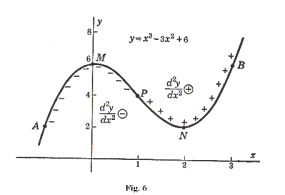
In Fig. 6 we see the graph of the function

y = x³ - 3x² + 6 .

On the arc AMP the value of d²y/dx² is negative and on the arc PNB it is positive. Point P where it changes form negative to positive is an inflection point.

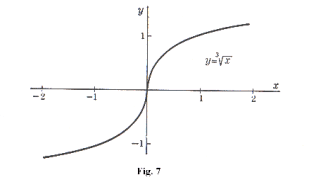
Inflection point. An inflection point on a curve is a point at which the second derivative d²y/dx² changes sign (i.e. from negative to positive or positive to negative). Thus it is a point at which the concavity of the curve changes (from upward concavity to downward concavity or vice versa). In general, d²y/dx² = 0 at inflection points. However, it is possible for a curve to have an inflection point at which d²y/dx² is not equal to zero. This can only happen, however, if the second derivative fails to exist at such a point. Such points can be discovered by studying the behavior of the curve in the neighborhood of any points at which d²y/dx² becomes infinite or otherwise fails to exist. An example of a curve with an inflection point where d²y/dx² is not equal to zero is the curve

shown in Fig. 7. The derivatives are

There is no value of x for which d²y/dx² = 0, but the derivative fails to exist at x = 0. The point (0, 0) is an inflection point. To the left of the point d²y/dx² is positive and the curve is concave upward and to the right of the point d²y/dx² is negative and the arc is concave downward.

Def. Critical (or stationary) point. A critical (or stationary) point of a function y = f(x) is a point at which dy/dx = 0. It corresponds to a point on the curve at which the tangent to the curve is horizontal.

● In general, a critical point represents either a maximum point, a minimum point or an inflection point.

Def. Critical value of x. A value of x at which a critical point occurs i.e. a point at which dy/dx = 0. All roots of f '(x) = 0 are critical values of x.

Maxima and minima. A function y = f(x) has a maximum at a point x₀ if f(x₀) f(x) for all points in the neighborhood of x₀. Such a function has a minimum at a point x₀ if f(x₀) f(x) for all points in the neighborhood of x₀.

Necessary condition for a maxima or minima. Generally speaking, a necessary condition for a function y = f(x) to have a maximum or minimum at a point is that dy/dx = 0 at the point. However, there is an exception. In Fig. 8 point E represents an exception. At point E dy/dx doesn’t exist. Maxima or minima can occur at points at which dy/dx doesn’t exist.

Referring to Fig. 8:

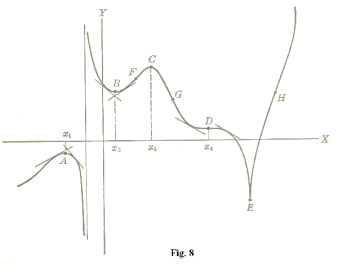
● A, B, C, D are critical (or stationary) points; dy/dx = 0 at each point A, B, C, D

● x₁, x₂, x₃, x₄ are critical values of x

● A and C are maximum points

● B and E are minimum points

● F, G, D and H are inflection points

Procedure for determining maxima and minima. In locating maximum and minimum points we utilize the following fact: The slope is positive immediately before (to the left of) a maximum point and negative immediately after one. For a minimum point, the slope is negative before and positive after.

To determine the maximum and minimum points of y = f(x):

1. Solve f '(x) = 0 for the critical values of x.

2. Apply either the first derivative test or second derivative test:

First derivative test:

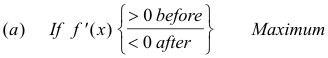
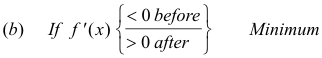
If neither (a) nor (b) holds, then the point in question is neither a maximum nor a minimum but a point of inflection with a horizontal tangent.

Second derivative test:

f ''(x₁) < 0 — Maximum point

f ''(x₁) > 0 — Minimum point

If f ''(x₁) = 0, the test fails and the point might or might not be a maximum or minimum. In this case we can proceed as follows. Let

f '(x₁) = f ''(x₁) = f ''' (x₁) = ... = f ^{[n -1]}(x₁) = 0,

f ⁿ(x₁) 0.

Then

(a) n is even. If f ⁿ(x₁) < 0, point is a maximum

If f ⁿ(x₁) > 0, point is a minimum

(b) n is odd. Point is neither a maximum nor a minimum.

Example. Find the maxima and minima of

y = 2x³ + 3x² - 12x - 15

See Fig. 9.

Solution.

y' = 6x² + 6x - 12

= 6(x+2)(x - 1) = 0

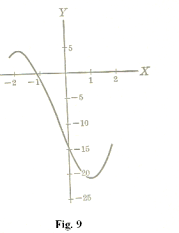
Critical values: x = -2, 1

First derivative test for x = -2 :

y' > 0 before, y' < 0 after

Thus x = -2 corresponds to a maximum point.

First derivative test for x = 1 :

y' < 0 before, y' > 0 after

So x = 1 corresponds to a minimum point.