Website owner:  James Miller

MEAN VALUE THEOREMS FOR DERIVATIVES; ROLLE’S THEOREM, MEAN VALUE THEOREM, CAUCHY’S GENERALIZED MEAN VALUE THEOREM, EXTENDED LAW OF THE MEAN (TAYLOR’S THEOREM)

In the following we present several mean value theorems for derivatives. The functions referred to are general functions (not just functions defined by expressions or formulas).

Rolle’s Theorem. Let f(x) be a function which is continuous over the interval a x b and has a derivative at every interior point of the interval. Then if f(a) = f(b) = 0, there must be at least one point x₁ between a and b for which f '(x₁) = 0.

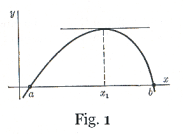
Geometrically, the theorem means that if a continuous curve intersects the x-axis at x = a and x = b, and has a tangent at every point between a and b, then there is at least one point x = x₁, between a and b where the tangent is parallel to the x-axis. See Fig. 1.

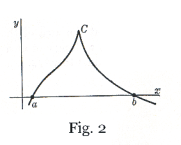
If f(x) does not have a derivative at every point of the interval, the theorem doesn’t apply and there may not be any point between a and b for which f '(x) = 0. See Fig. 2.

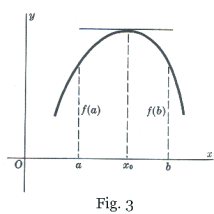
Corollary. If f(x) satisfies the conditions of Rolle’s Theorem, except that f(a) = f(b) 0 , then f '(x) = 0 for at least one value of x, say x = x₀, between a and b. See Fig. 3.

Mean value theorem. Let f(x) be a function which is continuous over the interval a x b and has a derivative at every interior point of the interval. Then there must be at least one point x₁ between a and b such that

Syn. Law of the Mean

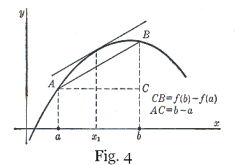
The theorem is geometrically obvious. See Fig. 4. The slope of the chord AB is

The theorem simply states that under the conditions specified there must be a point on the curve between A and B where the slope of the curve is equal to the slope of AB.

Proof of the Mean value Theorem. In proving this theorem we perform a stunt of magic. We pull a strange, nonsensical looking function out of a magic hat and present it to the reader. Noting that it meets the conditions required by Rolle’s Theorem, we apply Rolle’s Theorem to it and voila! The reader is staring at the required proof!

The function that we pull out of a hat and present to the reader is

We note that it meets the requirements of Rolle’s Theorem: F(a) = 0 , F(b) = 0 and if f(x) satisfies the conditions on continuity and differentiability specified in Rolle’s Theorem, then F(x) satisfies them also. Rolle’s Theorem requires the expression for F '(x). Taking the derivative of F(x)

Rolle’s Theorem states that for some value x = x₁ between a and b

Thus

and the theorem is proved.

Cauchy’s Generalized Mean Value Theorem. Let f(x) and g(x) be two functions which are continuous on the closed interval [a, b] and differentiable on the open interval (a, b). Assume further that g(a) g(b) and that f '(x) and g'(x) are never simultaneously zero at any point on the open interval (a, b). Then there exists a point x₁ in (a, b) such that

Syn. Generalized Law of the Mean, Double Law of the Mean, Cauchy’s Mean Value Formula

A geometrical interpretation may be given for the theorem as follows: Let a plane curve be represented parametrically by the equations

            x = g(t)

            y = f(t) 

where a t b. See Fig. 5. The slope of the curve for a given t is

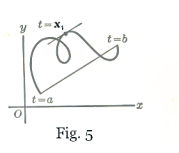
The constant  

is the slope of the straight line joining the points on the curve corresponding to t = a and t = b, respectively. The theorem says that the two slopes 1) and 2) are equal for at least one value of t between a and b.

Proof of Cauchy’s Generalized Mean Value Theorem. In proving this theorem we again perform a stunt of magic. We pull a strange, nonsensical looking function out of thin air and present it to the reader. Noting that it meets the conditions required by Rolle’s Theorem, we apply Rolle’s Theorem to it and voila! The reader is staring at the required proof!

The function that we pull out of a hat and present to the reader is

We note that it meets the requirements of Rolle’s Theorem: F(a) = 0 , F(b) = 0 and if f(x) and g(x) satisfy the conditions on continuity and differentiability specified in Rolle’s Theorem, then F(x) satisfies them also. Rolle’s Theorem requires the expression for F '(x). Taking the derivative of F(x)

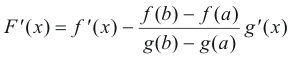
Rolle’s Theorem states that for some value x = x₁ between a and b

Rearranging we obtain

and the theorem is proved.

Extended law of the mean. Let a function f(x) and its first n derivatives be continuous on the closed interval [a, b] and let the (n+1)st derivative f ^{(n + 1)}(x) exist on the open interval (a, b). Then there is a number x₀ between a and b such that

in which R_n+1(x), the remainder after n + 1 terms, is given by the formula

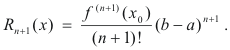
When b is replaced by the variable x, 4) becomes

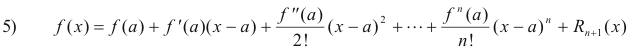
in which R_n+1(x), the remainder after n + 1 terms, is given by the formula

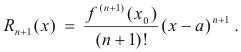
Formula 5) can be recognized as Taylor’s Formula. The Extended Law of the Mean is a variation of Taylor’s Formula.

Proof of the Extended Law of the Mean. We now present the proof of 4) above. In proving this theorem we again perform our stunt of magic. This time we pull two strange looking functions out of thin air and present them to the reader. Noting that the two functions meet the conditions required by Cauchy’s Generalized Mean Value Theorem, we apply the theorem and, in a step or two, have the proof.

The functions that we pull out of a hat and present to the reader are

We observe that these two functions meet the requirements of Cauchy’s Generalized Mean Value Theorem. We also observe that F(b) = G(b) = 0. To use Cauchy’s theorem we need the expressions for F'(x) and G'(x). When we differentiate F(x) we discover that a great deal of cancellation occurs between terms. The derivative of F(x) is found to be

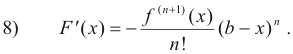
The derivative of G(x) is

We now apply Cauchy’s Mean Value Theorem. Since F(b) and G(b) are zero, it reads

or

where x₀ is some number between a and b. Substituting 7), 8) and 9) into 11) we get

If we now put x = a in 6) and use 12) we obtain the desired formula 4) above.