The dihedral group of the square

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

THE DIHEDRAL GROUP OF THE SQUARE

Consider a cardboard square as shown in Figure 1. There are eight motions of this square which, when performed one after the other, form a group called the Dihedral Group of the Square. They are:

I – 0⁰ rotation (clockwise, about center O, in plane of cardboard)

R – 90⁰rotation (clockwise, about center O, in plane of cardboard)

R₁ – 180⁰ rotation (clockwise, about center O, in plane of cardboard)

R₂ – 270⁰ rotation (clockwise, about center O, in plane of cardboard)

H – reflection about horizontal axis AB (180⁰ flip through space)

V – reflection about vertical axis EF (180⁰ flip through space)

D – reflection about diagonal 1-O-3 (180⁰ flip through space)

D₁ – reflection about diagonal 2-O-4 (180⁰ flip through space)

The Dihedral Group of the Square then is given by G = [ I, R, R₁, R₂, H, V, D, D₁ ]. Multiplication in G consists of performing two of these motions in succession. Thus the product HR corresponds to first performing operation H, then operation R. A multiplication table for G is shown in Figure 2. Entries in the table contain the product XY where X corresponds to the row and Y corresponds to the column. Thus in the table HR = D₁.

The eight motions I, R, R₁, R₂, H, V, D, D₁ can be represented as permutations of the numbers 1, 2, 3, and 4 where these numbers correspond to the four corners of the square as shown in Figure 1. Figure 3 shows their permutation representation. Thus G can also be represented as the set

G = [ (1), (1432), (13)(42), (1234), (14)(23), (12)(43), (42), (13) ]

of permutations of the vertices. In this case multiplication corresponds to the multiplication of permutations.

I	(1)	0⁰ rotation
R	(1432)	90⁰rotation
R₁	(13)(42)	180⁰ rotation
R₂	(1234)	270⁰ rotation
H	(14)(23)	reflection about horizontal axis AB
V	(12)(43)	reflection about vertical axis EF
D	(42)	reflection about diagonal 1-O-3
D₁	(13)	reflection about diagonal 2-O-4

Figure 3

Subgroups The subgroups of G are shown in Figure 4 along with their relationship to one another.

_________________________________________________________

_________________________________________________________

Group G is not cyclic. It is generated by the two elements R and H. From the multiplication table it can be seen that

R⁰ = I R = R R² = R₁ R³ = R₂

H⁰ = I H = H HR = D₁ HR² = V HR³ = D

Thus we see that the elements of G can be represented uniquely as HⁱR^jwith i = 0,1 and

j = 0, 1, 2, 3 i.e.

H⁰R⁰ = I H⁰R¹ = R H⁰R² = R₁ H⁰R³ = R₂

H¹R⁰ = H H¹R¹ = D₁ H¹R² = V H¹R³ = D

Def. Automorphism. An automorphism of a group G is a one-to-one mapping f :G → G (i.e. a one-to-one correspondence between elements of G) where f(ab) = f(a)f(b) for all a,b in G. It represents an isomorphism of group G with itself.

Theorem. For any fixed element x of a group G, the mapping T_x(a) : a → x ^-1ax carrying a into x ^-1ax effects an automorphism on G. Each x ∈ G gives a different automorphism.

Thus this theorem says that the mapping T_x(a) : a → x ^-1ax establishes a correspondence between members of G in which, for any selected x ∈ G, f(ab) = f(a)f(b) for all a,b in G.

Proof. We need to prove that for any x in G, f(ab) = f(a)f(b) for all a,b in G. Thus we need to prove x^-1(ab)x = (x^-1ax)(x^-1bx) for all a,b in G. The proof follows immediately since (x^-1ax)(x^-1bx) = x^-1a(xx^-1)bx = x^-1abx.

Let H = {h₁, h₂, .... ,h_n} be a subgroup of G. For a fixed x ∈ G, apply the transform T_x(a) : a → x ^-1ax to all elements h₁, h₂, .... ,h_n of H mapping them into elements k₁, k₂, .... ,k_n. in G. The elements k₁, k₂, .... ,k_n then correspond to a subgroup K of G that is isomorphic to H. Each element k_i ∈ K is a conjugate of its counterpart h_i ∈ H. Group K is said to be conjugate to H. Thus, in general, the transform T_x(a) : a → x ^-1ax effects a automorphic mapping from one subgroup of G into another subgroup of G. Each x_i ∈ G gives a different automorphic mapping of group H, mapping H into another (or perhaps the same) subgroup of G. The set of all subgroups into which the transform T_x(a) : a →x ^-1ax maps H for all the different x_i ∈ G is a set of subgroups conjugate to H. Any two of the subgroups are conjugate to each other.

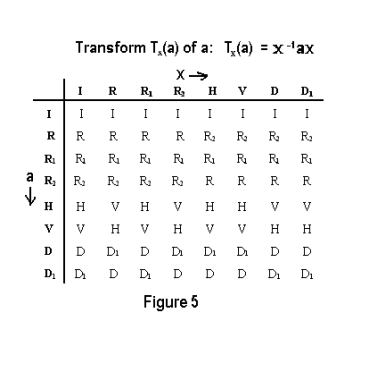
Transforms. In Figure 5 we see a table giving the transforms of each element a of G for each value of x. Computation of the Table of Transforms. If we read across on the rows we see the conjugates of each element a. Thus the rows represent the different conjugate classes into which the group is partitioned. All elements in a particular row are conjugate to each other. In some cases different rows give the same conjugate class. We can list the conjugate classes:

class 1 = { I }

class 2 = { R, R₂ }

class 3 = { R₁ }

class 4 = { H, V }

class 5 = { D, D₁ }

The subgroups of G are [I, D, D₁, R₁], [I, R₁, R₂, R₃], [I, H, V, R₁], [I, D], [I, D₁], [I, R₁], [I, H], [I, V]. Let us now consider what these eight subgroups are mapped into by the transform T_x(a) : a → x ^-1ax for different values of x. Each subgroup under the transform T_x(a) : a → x ^-1ax for x = x_i is mapped into another subgroup that is isomorphic to it. What is the subgroup [I, D, D₁, R₁] mapped into under the transform for x = R? We read from the second column of Table 5 to find the images of the individual elements. We see that I → I, D → D₁, D₁ → D, R₁ → R₁. Thus subgroup [I, D, D₁, R₁] is mapped into [I, D, D₁, R₁] i.e. it is mapped into itself. What is subgroup [I, H] mapped into for x = R? It is mapped into [I, V]. Likewise, subgroup [I, D] is mapped into [I, D₁].

All of these automorphic mappings of the various subgroups of G for various values of x = x_i constitute the automorphisms of the group G and its subgroups.

References

Birkhoff, Mac Lane. A Survey of Modern Algebra. Chap. VI