Gradient, del operator, directional derivative

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

GRADIENT, DEL OPERATOR, DIRECTIONAL DERIVATIVE

Def. Gradient. Let Φ(x, y, z) be a scalar point function that is defined and differentiable at each point (x, y, z) in a certain region of space. The gradient of Φ is a vector point function defined as

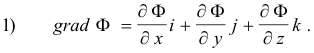
The gradient of Φ is also denoted by

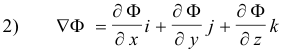
where ∇ is called the del operator.

Stated in words, the gradient of a scalar point function Φ(x, y, z) is a vector whose components along the x, y, z axes are the partial derivatives of Φ(x, y, z) with respect to the variables.

Def. Del operator. The del operator ∇ is defined by

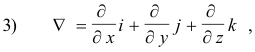
something that has no meaning by itself. It is a contrivance that is useful in working with vector functions. It is used in defining the gradient, divergence and curl and is a thing which is convenient because it can be treated as if it were a vector in working with vector functions. It obeys vector laws and when combined with vectors gives meaningful results. It is a convenient device. It is also known as nabla.

Gradient. Physical interpretation. The gradient, at any point P:(x, y, z), of a scalar point function Φ(x, y, z) is a vector that is normal to that level surface of Φ(x, y, z) that passes through point P. The magnitude of the gradient is equal to the rate of change of Φ (with respect to distance) in the direction of the normal to the level surface at point P.

Grad Φ, evaluated at a point P:(x₀, y₀, z₀), is normal to the level surface Φ(x, y, z) = c passing through point P. The constant c is given by c = Φ(x₀, y₀, z₀).

Directional derivative of a scalar point function. The rate of change (i.e. derivative) of a scalar point function Φ in some specified direction is called the directional derivative in that direction.

The rate of change (with respect to distance) of Φ(x, y, z) at a point P in some specified direction is as follows: Let the direction be specified by a unit direction vector a. Then the rate of change of Φ in the direction of a is given by

grad Φ∙ a

i.e. the dot product of grad Φ and a. In other words,

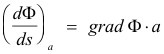
where

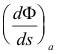
is the directional derivative of Φ in the direction of unit vector a.

Proof

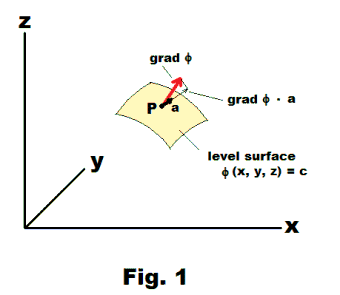
Thus the rate of change of Φ in the direction of a unit vector a is the component of grad Φ in the direction of a (i.e. the projection of grad Φ onto a ). See Fig. 1. The maximum value of the directional derivative occurs when the directional vector a coincides with the direction of grad Φ. Thus the directional derivative achieves its maximum in the direction of the normal to the level surface Φ(x, y, z) = c at P.