Matrix representation of a linear transformation

SolitaryRoad.com

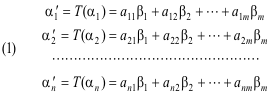
Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

Let V be some abstract n-dimensional vector space over field F and let W be an abstract m-dimensional vector space over field F. Let B = {α₁, α₂, .... , α_n} be a basis for V and B' = {β₁, β₂, .... , β_n} be a basis for W. Then any vector v in V can be expressed in terms of its coordinate vector (a_1, a₂, ... , a_n ) and basis {α₁, α₂, .... , α_n} as v = a₁α₁ + a₂α₂ + .... + a_nα_n . Similarly, any vector w in W can be expressed in terms of its coordinate vector (b_1, b₂, ... , b_n ) and basis {β₁, β₂, .... , β_n} as w = b₁β₁ + b₂β₂ + .... + b_nβ_n .

Let T: V →W be a linear transformation from V into W. Let α₁', α₂', .... , α_n' be the images in W under transformation T of the basis vectors α₁, α₂, .... , α_n as referred to the W basis B' ={β₁, β₂, .... , β_n}:

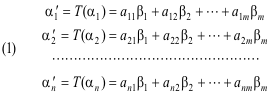
or, in matrix form,

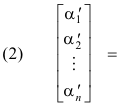
Matrix representation of T relative to the bases B and B'. The matrix representation of T relative to the bases B and B' is given by the transpose of the above matrix of coefficients i.e.

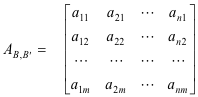
The i-th column of mxn matrix A_B,B' consists of the coordinates in W space of the image of the i-th basis vector with respect to the B' basis. The significance of A_B,B is given in the following theorem:

Theorem. If T is a linear transformation T: V → W from an abstract n-dimensional space V to an m-dimensional space W and mxn matrix A_B,B' is the matrix representation of the transformation, then for any vector v V

where [v]_B is the coordinate vector of v as referred to the B basis and [T(v)]_B' is the coordinate vector of the image of v (in W) as referred to the B' basis.

Thus if we multiply the coordinate vector of v by the matrix representation of T, we obtain the coordinate vector of the image of v.

A special case of the above is the case where we map an n-dimensional vector space V onto itself, T: V →V and B’ = B. In this case the matrix representation of T is n-square.

Example. Let V be the space of all polynomials

of degree ≤m over the field F of real numbers and let B = {1, x, x², ... , xⁿ} be a basis for the space. Let T: V →V be a linear mapping on V. The images of the n = m + 1 basis vectors

1, x, x², ... , xⁿ are given by

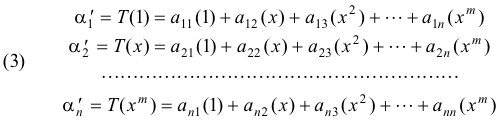
or, in matrix form,

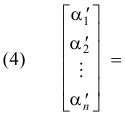
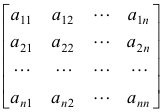
The matrix representation of T relative to the basis B is then given by the transpose of the matrix of coefficients of (4):

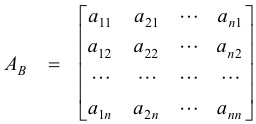
Suppose now that V is the vector space of polynomials

of degree 3 over field R of real numbers and suppose that the linear mapping T is that of the differential operator D defined by

The basis vectors α₁, α₂, .... , α_n are 1, x, x², ... , xⁿ .

Upon taking the derivatives of the basis vectors

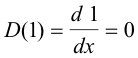
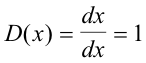
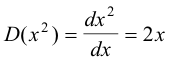
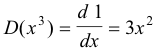
equations (1) above then become

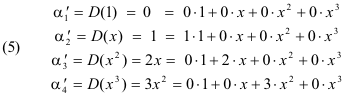
or, in matrix form,

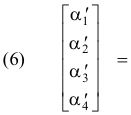
The matrix representation of the linear transformation effected by the differential operator D relative to the basis B is then given by the transpose of the matrix of coefficients in (6)

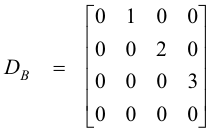
References

Lipschutz. Linear Algebra. p.156

Hoffman, Kunze. Linear Algebra. p. 79,80