Elementary operations on lambda matrices, Equivalence, Smith normal form, invariant factors, elementary divisors

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

Elementary operations on λ-matrices. The elementary operations on λ-matrices are the same as those for regular matrices, except in Operation 3 the word “constant” is replaced by “polynomial”. An elementary operation on a λ-matrix over polynomial domain F(λ) consists of one of the following operations:

1. Interchanging any two rows or any two columns.

2. Multiplying any row or column by a non-zero constant.

3. Adding to any row the product of any arbitrary polynomial p(x) of F(λ) times another row or adding to any column the product of any arbitrary polynomial p(x) of F(λ) times another column.

We denote the different operations as follows:

H_ij – interchange of the i-th and j-th rows

K_ij – interchange of the i-th and j-th columns

H_i(k) – multiplication of the i-th row by the non-zero constant k

K_i(k)– multiplication of the i-th column by the non-zero constant k

H_ij(p(λ)) – addition to the i-th row the product of p(λ) times the j-th row

K_ij(p(λ)) – addition to the i-th column the product of p(λ) times the j-th column

As with regular matrices, corresponding to each operation is an elementary matrix, obtained by performing the elementary operation on the identity matrix I_n. And it works in the same way as with regular matrices – multiplication by the elementary matrix effects the same transformation as does the operation. We will denote the elementary matrix by the same symbol as we use for the operation.

The following theorems parallel those for regular matrices:

1] Every elementary matrix has an inverse which in turn is an elementary matrix.

2] Every non-singular λ-matrix can be expressed as a product of elementary matrices.

3] The rank of a λ-matrix is invariant under elementary operations.

Equivalence of λ-matrices. Two n-square λ-matrices A(λ) and B(λ) with elements in polynomial domain F[λ] are called equivalent provided there exist non-singular matrices P(λ) and Q(λ) such that

Two mxn λ-matrices are equivalent if and only if they have the same rank.

Theorem. Let A(λ) and B(λ) be equivalent matrices of rank r. Then the greatest common divisor of all s-square minors of A(λ), s ≤ r, is also the greatest common divisor of all s-square minors of B(λ).

Smith Normal Form. The Smith Normal Form is a canonical matrix of the form

where

1) Each f_i(λ) is a monic polynomial in λ (i.e. each f_i(λ) is a polynomial in which the coefficient of the highest power of λ is unity)

2) Each f_i(λ) divides f_i+1(λ) (i = 1, 2, ....., r-1)

Theorem. Every λ-matrix A(λ) of rank r can be reduced to the Smith Normal Form by elementary row and column transformations.

That Smith normal matrix N(λ) to which a given matrix A(λ) reduces by elementary row and column transformations is uniquely determined by A(λ). Thus the Smith normal matrices form a canonical set for equivalence over F(λ).

Invariant factors of a Lambda-matrix. The monic polynomials f₁(λ), f₂(λ), .... , f_r(λ) in the diagonal of the Smith normal form of a Lambda-matrix are called the invariant factors of the Lambda-matrix.

Trivial invariant factors of a Lambda-matrix. If an invariant factor of a Lambda-matrix is “1" it is called a “trivial invariant factor”. The first several diagonal elements in the Smith normal form of a Lambda-matrix may be “1" as in

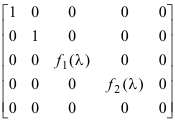
If f_k(λ) = 1, k ≤ r, then f₁(λ) = f₂(λ) = .... = f_k(λ) = 1.

Theorem. Two n-square λ-matrices over F[λ] are equivalent over F[λ] if and only if they have the same invariant factors.

Elementary divisors of a Lambda-matrix. Each invariant factor of an n-square

λ-matrix over f[λ] can be expressed as a product of factors which are irreducible with respect to some number field (i.e. the field of rationals, reals, etc.). Since these irreducible factors may occur in multiples (i.e. powers of an irreducible factor may occur) we can say that an invariant factor f(λ) can be expressed in terms of its irreducible factors as

where p₁(λ), p₂(λ), .... , p_n(λ) are distinct, monic, irreducible polynomials of F[λ].. Each quantity

is called an elementary divisor of the corresponding Lambda-matrix. Thus an elementary divisor of a Lambda-matrix is an irreducible factor as raised to some power (the power being the number of times it occurs as a factor of the corresponding invariant factor).

Note. Over the complex field each invariant factor f(λ) can be expressed as a product of the type

where λ₁, λ₂, .... , λ_n are distinct. Each factor is an elementary divisor of the Lambda-matrix.

Example. Suppose a 10-square λ-matrix A(λ) over the rational field has the Smith normal form

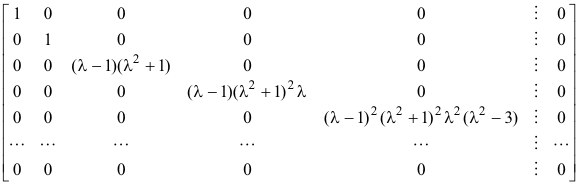
The rank is 5.

The invariant factors are

The elementary divisors are:

Note that the elementary divisors are not necessarily distinct; In the listing each elementary divisor appears as often as it appears in the invariant factors.

Theorem. Two n-square λ-matrices over F[λ] are equivalent over F[λ] if and only if they have the same rank and the same elementary divisors.

References

Ayres. Matrix Theory. Chap. 24

Bocher. Introduction to Higher Algebra. Chap. XX