The solution set of the linear system AX = 0 is a vector space

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

The solution set of the linear system ax = 0 is a vector space

Consider the system of m linear equations in n unknowns x₁, x₂, .... ,x_n

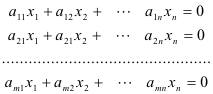
or, more concisely, AX = 0. Let the rank of the coefficient matrix A be r. If r = n the solution consists of only the single solution X = 0, which is called the trivial solution. If r < n there are an infinite number of solution vectors which will satisfy the system corresponding to all points in some subspace of n-dimensional space. To illustrate this let us consider a couple of simple examples from ordinary three-dimensional space.

Suppose the system AX = 0 consists of the single equation

5x + 3y + 9z = 0 .

This equation corresponds to a plane in three-dimensional space that passes through the origin of the coordinate system. Any point on this plane satisfies the equation and is thus a solution to our system AX = 0. The set of all solutions to our system AX = 0 corresponds to all points on this plane. Furthermore, since the plane passes through the origin of the coordinate system, the plane represents a vector space. Why? Because a linear combination of any two vectors in the plane is also in the plane and any vector in the plane can be obtained as a linear combination of any two basis vectors in the plane. So, in summary, in this particular example the solution set to our system AX = 0 corresponds to the two-dimensional subspace of three-dimensional space represented by this plane. We call this subspace the solution space of the system AX = 0.

Let us consider another example. Suppose the system AX = 0 consists of the following two equations

2x + 5y + 3z = 0

9x - 2y - 8z = 0

These two equations correspond to two planes in three-dimensional space that intersect in some line which passes through the origin of the coordinate system. Any point of this line of intersection satisfies the system and is thus a solution to our system AX = 0. Furthermore, since the line passes through the origin of the coordinate system, the line represents a vector space. A linear combination of any two vectors in the line is also in the line and any vector in the line can be obtained as a linear combination of any basis vector for the line. So, in summary, in this example the solution set to our system AX = 0 corresponds to a one-dimensional subspace of three-dimensional space represented by this line of intersection of the two planes. In this case the solution space of the system AX = 0 is one-dimensional.

What determines the dimension of the solution space of the system AX = 0? The dimension is given by n - r. In our first example the number of unknowns, n, is 3 and the rank, r, is 1 so the dimension of the solution space was 3 - 1 = 2. In our second example n = 3 and r = 2 so the dimension of the solution space was 3 - 2 = 1.

Theorem. The solution set of the linear system AX = 0 is a vector space. This means that if X₁ and X₂ are any two solution vectors of AX = 0 and k₁ andk₂are arbitrary constants then

X = k₁X₁ + k₂X₂

is also a solution vector of the system.

Proof. Since X₁ and X₂ are solutions, AX₁ = 0 and AX₂ = 0. Thus

AX = A(k₁X₁ + k₂X₂) = k₁AX₁ + k₂AX₂ = k₁·0 + k₂·0 = 0 .

If r < n the solution space of AX = 0 is multi-dimensional of dimension n - r. If it has a dimension of s there will exist s linearly independent basis vectors that span the space. Any solution of the system can be written as some linear combination of these basis vectors. In general, the solution space of AX = 0 is some s-dimensional subspace of n-space. In 3-space it consists of some line or plane that passes through the origin of the coordinate system. Now let us note that although the solution set of AX = 0 does constitute a vector space the solution set of AX = B does not constitute a vector space. It is not true that if X₁ and X₂ are two solution vectors of AX = B and k₁ and k₂ are arbitrary constants that

X = k₁X₁ + k₂X₂

is a solution of the system. It is true that the solution set of AX = B may correspond to some line or plane of points in n-dimensional space but the line or plane doesn't pass through the origin of the coordinate system and does not represent a vector space. Only those lines or planes that pass through the origin represent vector spaces. Only they represent vector subspaces of n-dimensional space -- lines and planes not passing through the origin do not.

The solution space of the linear system AX = 0 is called the null space of matrix A. It is called this because if we view matrix A as a linear operator it images all points of this solution space into the null vector "0".