Interference and diffraction of light waves. Young�s experiment. Newton�s rings. Diffraction by a single slit. Diffraction gratings.

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

Interference and diffraction of light waves. Young’s experiment. Newton’s rings. Diffraction by a single slit. Diffraction gratings.

Interference of light waves. Light waves can interfere with one another in the same way that two water waves approaching each other in a pond can interfere with one another. See Fig. 1. As with water waves, there can be either constructive or destructive interference. The resulting wave is given by the following general superposition principle that applies to all waves:

Principle of superposition of waves. The principle of superposition of waves states that when two or more waves pass through the same point, the total displacement at that point is equal to the sum (vector sum) of the displacements produced by the individual waves.

Constructive and destructive interference. When two waves meet at a point their amplitudes are added. The waves may enhance each other, giving a resultant amplitude of greater magnitude, or they may tend to cancel each other out, giving a resultant amplitude of lesser magnitude, depending on whether their amplitudes are of the same or opposite sign. If they enhance each other, we have constructive interference at the point and if they tend to cancel each other out, we have destructive interference at the point.

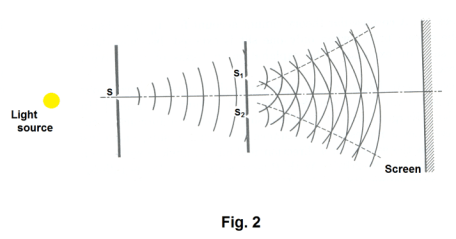
Young’s experiment. One of the earliest demonstrations of the fact that light waves can interfere with one another in a way similar to water waves was an experiment of English scientist Thomas Young in 1800. A diagram of the experiment is shown in Fig. 2. A monochromatic light source illuminates a narrow horizontal slit S. S₁ and S₂

are very fine horizontal slits, equidistant from S, and separated from each other by a very short distance of perhaps 0.25 mm (they are shown further apart in the figure for clarity). When a screen is placed at a large distance from S₁ and S₂, alternate bright and dark bands, called interference fringes, appear on the screen. See Fig. 3. By measuring the distance from the central fringe to some fringe on either side, we can compute the wavelength of the light.

The slits S₁ and S₂ act as two new light sources emitting light of the same frequency and phase in arced wavelets similar to those produced when a pebble is dropped in a pond (to insure that we have two light sources that are of the same frequency and phase it is necessary to start with a single light source and split it).

The bright fringes correspond to areas where the wavelets from S₁ and S₂ are in phase. Let P be a point at the center of one of the upper bright fringes, representing a point of complete reinforcement. See Fig. 4. Then the light path distance from S₂to P must exceed the distance from S₁ to P by an integral number of wavelengths i.e.

S₂P - S₁P = mλ

where m is an integer. We can find this path difference by swinging an arc of radius S₁P about P to intersect the line S₂P at A. The path difference is S₂A. Because we are dealing with extremely small angles, we can approximate the arc by the chord S₁A. Also, we can assume that S₁A is perpendicular to S₂P at A.

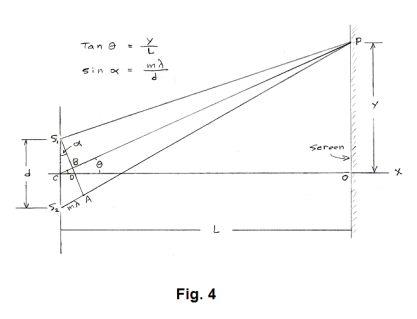
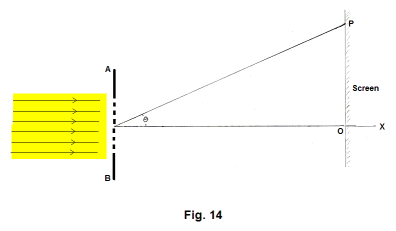
In the observed band of interference fringes, the middle bright fringe (the central fringe) is located at point O on the x axis in Fig. 4. It corresponds to a point of zero path difference and a value of m = 0. Let y be the distance from O (the center of the central bright fringe) to P, L be the distance CO from the source slits to the screen, and d be the distance separating the source slits, as shown in the figure. Then from the figure we see that

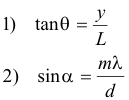
From triangle S₁CD we note that α is complementary to ∠CDS₁ and from triangle CDB we note that θ is complementary to ∠CDS₁. Therefore we conclude that α = θ. We can thus write 2) as

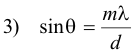
For very small angles such as the ones we are dealing with, sin θ = tan θ. Thus, from 1) and 3), we get

Hence, from measurements of y, d, and L, we can compute the wavelength λ.

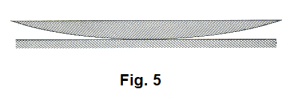
Newton’s rings. Newton observed and studied the interference produced when the convex surface of a lens is placed in contact with a plane glass plate. See Fig. 5. If the lens is only very slightly convex, the wedge-shaped film of air between them is about as thick as the length of a light wave near the point of contact. Monochromatic light, such as that from a sodium vapor lamp, will create an interference pattern consisting of a series of bright and dark rings as shown in Fig. 6. The wedge-shaped film of air of varying thickness causes some of the reflected waves to meet in the same phase and others to meet in opposite phase.

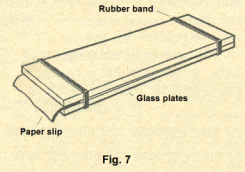
A very simple apparatus for demonstrating interference bands is shown in Fig. 7. It consists of two glass plates with a slip of paper inserted between them at one end, thus creating a very thin wedge-shaped film of air between them. When illuminated with monochromatic light, a series of parallel bright and dark lines will be seen.

Interference in thin films. The colors seen in soap films, oil slicks and butterfly wings are due to interference effects from light reflecting from both front and rear surfaces of the film or membrane. What happens, whether constructive or destructive interference occurs, depends on the thickness of the film and the wavelength of the light traveling within the film.

Let t be the thickness of the film, n be its index of refraction, and λ' be the wavelength of light

within the film. If the wavelength of the light in air is λ, then λ' = λ/n. The light travels a distance of 2t in its passage from the front surface to the rear surface of the film and then back. The difference in phase between the light reflected from the front and the rear surfaces of the film is given by

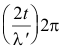
In addition, if the light is incident on the front surface at an angle that is normal or near normal, there is a phase shift of 180^o or π. Thus the total phase shift Δφ is given by

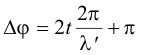
or, substituting in λ' = λ/n,

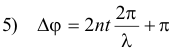
When the phase difference between the two reflected beams (from front and rear surfaces) is a multiple of 2π, the beams reinforce each other; when the phase difference is an odd multiple of π, the beams interfere destructively and no light is reflected from the film.

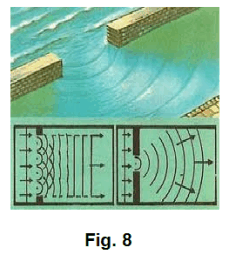
Diffraction of light. Diffraction is the spreading or bending of waves as they bend around the edge of an obstacle or pass through an opening whose dimensions are comparable to the wavelength of the wave. Diffraction occurs with all waves — water waves, sound waves, light waves, X-Rays, radio waves. Sea waves will spread out when coming through an opening in a breakwater. See Figures 8 and 9. The diffraction of light is the phenomenon in which, under certain

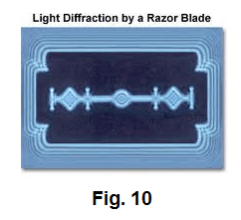
circumstances, light will bend around edges or obstacles to a small but appreciable extent. Fig. 10 shows a diffraction pattern produced by a razor blade. The photograph was made by placing a razor blade halfway between a pinhole illuminated by monochromatic light and a photographic film. The light bent around the edges of the razor blade creating an interference pattern. The reason a diffraction pattern like this would not usually be seen in the shadow of a razor blade is simply that most light sources are not point sources. If the light source were a frosted incandescent bulb, for example, light from each point of the bulb would form its own diffraction pattern and these would overlap to such a degree that no individual patterns would be seen.

Diffraction effects are not commonly observed with light. One main reason is that the wavelength of light is much smaller than the dimensions of most common objects and diffraction doesn’t occur.

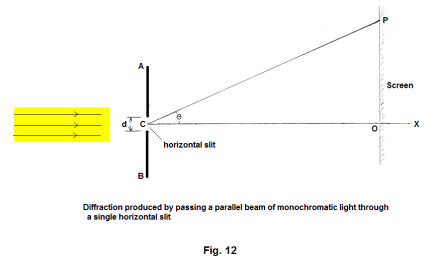
Diffraction by a single slit. Fig. 11 is a diffraction pattern obtained by focusing a beam of parallel monochromatic light on a single horizontal slit. Fig. 12 shows the setup. Point C is the center of the slit and CO is a line perpendicular to AB and the screen. Point P corresponds to the center of the m-th dark band (i.e. the point of total destructive interference in the m-th band). It can then be shown that

where λ is the wavelength of the light, d is the width of the slit, and θ is the angle between CO and CP.

Diffraction gratings. Suppose that instead of a single slit, or two slits as in Young’s experiment, we have a very large number of parallel slits all of the same width, and spaced at regular intervals. Such a device is called a diffraction grating. The first one, consisting of fine wires spaced at equal intervals, was constructed by Joseph Fraunhofer (1787 - 1826). Modern day diffraction gratings are constructed by ruling 10,000 to 30,000 lines per inch on flat glass or polished metal surfaces with a diamond point. Those ruled in flat glass are transmission gratings and those ruled in polished metal are reflection gratings. If sunlight is passed through a diffraction grating, the light is dispersed into a continuous spectrum (i.e. the solar spectrum) in the same way as with a prism. As a consequence it is often used instead of prisms in spectroscopes. Diffraction-grating spectroscopes are much used in spectroscopy because of certain advantages they have over prism spectroscopes.

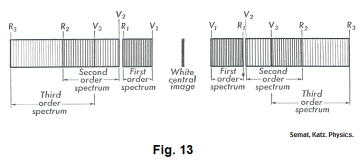
In contrast with the single spectrum produced by a prism, a grating forms a number of spectra on either side of the normal. Fig. 13 shows the relative positions of the first three orders of the spectra produced by a diffraction grating. Notice that they are reproduced on both sides of the white central image and that the second and third orders overlap substantially.

Referring to Fig. 14, assume (temporarily) that the incident light is monochromatic of wavelength λ and is directed normal to the plane of the grating. Let P represent the point at which light of this wavelength will undergo maximum constructive interference for a particular value of m, m = 0, 1, 2, 3, .... (where m corresponds to the order of the spectrum) and let θ be the angle between the normal to the plane of the grating and point P. Let d be the distance between the gratings. Then it can be shown that the value of θ is given by

If the incident light is polychromatic, we can use 7) to compute the value of θ for any given wavelength.

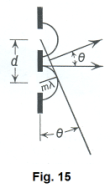
Fig. 15 shows the geometric situation that leads to equation 7). The situation shown in Fig. 15 represents the condition under which maximum constructive interference occurs. Maximum constructive interference occurs at the various values of m, m = 0, 1, 2, 3, ... .

References

Dull, Metcalfe, Brooks. Modern Physics

Sears, Zemansky. University Physics

Semat, Katz. Physics

Freeman. Physics Made Simple

Bennett. Physics (COS)