
Prove. For any angle θ,
![]()
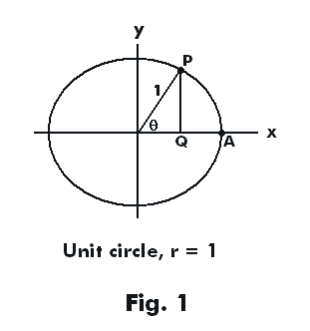
Proof. Consider the unit circle shown in Fig. 1. The angle θ, in radians, is equal to the distance along the circumference from point A to point P (i.e. it is equal to the length of the arc AP) and sin θ is equal to the perpendicular distance PQ. Obviously then, for all θ, PQ < AP. Consequently,
![]()