Problem. Derive the formula

where

and f(x) is a sectionally continuous function defined on an interval c < x < c + 2L

Derivation. In deriving the above formulas we will use the following definite integrals where m and n are positive integers. The integrals are valid for all values of c.

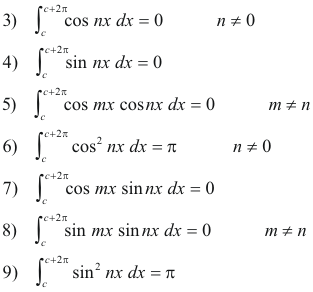
Step 1. We first consider the case of L = π i.e. the case where f(x) is a sectionally continuous function defined on an interval c < x < c + 2π. In this case 1) and 2) become

where

We will make a starting assumption that f(x) can be represented by series 10). We will not attempt to prove that here. We now give the derivation of the coefficients a_n and b_n of 11).

First, we shall assume that we can legitimately integrate 10) term by term (integrating a series term by term is not always legitimate). Integrating from x = c to x = c + 2π we get

The integral on the left can always be evaluated, since f(x) is a known function. If necessary some method of approximate integration such as the trapezoid rule can be used. The first term on the right is

By 3) all integrals with a cosine vanish and by 4) all integrals with a sine vanish. Thus 12) reduces to

or

To find a_n (n = 1, 2, 3, .....), we multiply each side of 10) by cos nx and then integrate from c to c + 2π to obtain

The integral on the left can always be evaluated. By 3) and 4) all the integrals on the right that contain only cosine terms are zero except the one containing cos² nx which, by 6), is equal to π. By 7) all the integrals containing sine terms are zero. Thus

or

We now determine b_n by essentially the same procedure. We multiply each side of 10) by sin nx and then integrate from c to c + 2π to obtain

we multiply each side of 10) by cos nx and then integrate from c to c + 2π to obtain            

As before all the integrals on the right vanish except for one, giving

or

Formulas 13), 14) and 15) are known as the Euler or Euler-Fourier formulas.

Step 2. In Step 1 we have proven that if the given function has a period of 2π, then its Fourier series representation is given by 10) and 11). We now deal with the following question: If the function f(x) that we are given has a period of 2L instead of 2π, what is its Fourier series representation? We will do a change of variable which effects a change of scale. We need the formula for the proper change of variable.

Let us first observe that the period p of a general function y = sin ax is given by p = 2π/a. See Fig. 1. The period corresponds to the range of values of x corresponding to a complete cycle of the function. Thus it is found by solving the equation ax = 2π for x i.e. p = 2π/a. (for example, the range of values of x corresponding to a complete cycle of the function y = sin 3.2x is found from the equation 3.2x = 2π so the period is x = 2π /3.2).

Thus the period of the functions sin ax and cos ax in a Fourier series is 2π/a. 

If the function f(x) that we wish to represent by a Fourier series has a period of 2L, then the a₁ and b₁ terms in its series representation must have the form a₁ cos ax and b₁ sin ax with a period of 2L = 2π/a. Thus a = π / L and the a₁ and b₁ terms are

We now ask ourselves the question: What change of variable that will change the given function f(x) into one with a period 2π? The answer: The change of variable that will accomplish this is t = πx/L, or x = Lt/π. If we make the substitution x = Lt/π in the given function y = f(x) we obtain a function

which has a period of 2π.

As a function of t of period 2π, F(t) is represented by the Fourier series

where

If, now, we make the inverse substitutions

in 16) and 17), they become

where

References.

  Wylie. Advanced Engineering Mathematics. Chap. 7