Prove. a) A necessary and sufficient condition for μ(x, y) to be an integrating factor for the equation

1)        M(x, y) dx + N(x, y) dy = 0

is that it satisfy the equation

Proof. Part 1. We first prove that if μ(x, y) is an integrating factor for 1) it must satisfy 2).

If μ(x, y) is an integrating factor for

            M dx + N dy = 0

then the equation

3)        μM dx + μN dy = 0 

must be exact. Therefore

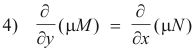
Consequently μ must satisfy the partial differential equation

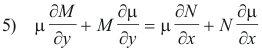
which, on rewriting, becomes

Part 2. We now show that if μ(x, y) satisfies 2) it must be an integrating factor for1).

If μ(x, y) satisfies 6) it must satisfy 4) also and thus it must be an integrating factor that makes 1) exact.

Prove. b) If

then

is an integrating factor for the equation

            M dx + N dy = 0.

Proof. Let μ be a function of x alone. Then ∂μ/∂y = 0 and ∂μ/∂x becomes dμ/dx. Then μ must satisfy 2) above and 2) then reduces to

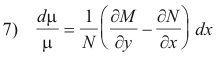
which becomes

8)        dμ/μ = f(x)dx

Integrating 8) gives

so

Prove. c) If

then

is an integrating factor for the equation

            M dx + N dy = 0.

Proof. Let μ be a function of y alone. Then ∂μ/∂x = 0 and ∂μ/∂y becomes dμ/dy. Then μ must satisfy 2) above and 2) then reduces to

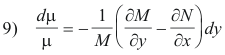
which becomes

10)      dμ/μ = -g(y)dy

Integrating 10) gives

so

References

1. Earl Rainville. Elementary Differential Equations.