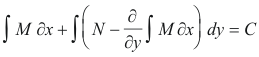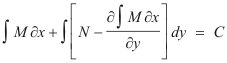
Derive: Formula for the general solution.

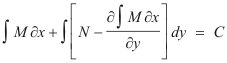
Derivation. We start with

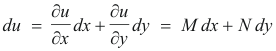
and

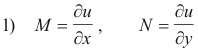
Let us now integrate M = ∂u/∂x partially with respect to x, keeping y constant. We obtain

where f(y) is an arbitrary function of y alone which corresponds to the usual constant of integration. Now taking the partial of 2) with respect to y we obtain

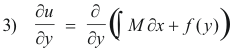
Since N = ∂u/∂y, 3) becomes

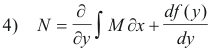
and rearranging we have

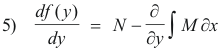
Since f(y) is a function of y alone, df(y)/dy is also a function of y alone and thus the right member of 5) does not contain x.

We now integrate 5) with respect to y to obtain

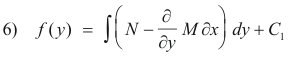
Now substituting 6) into 2) we obtain

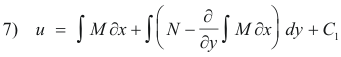
Thus the general solution is given by