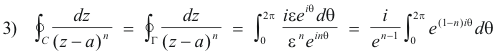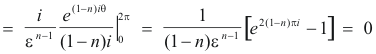Prove. Let C be a simple closed curve containing point a in its interior. Then

We prove the first part first.

I Prove: If C be a simple closed curve containing point a in its interior, then

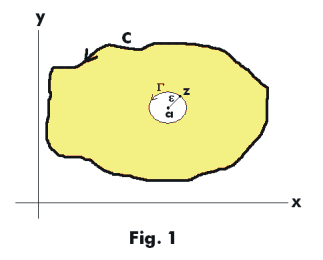
Proof. Construct a circle Γ of radius ε with center at a of such size that Γ lies entirely inside C (since a is an interior point it can be done). See Fig. 1. By the Principle of the Deformation of Contours we have

Now on Γ, |z - a| = ε and z - a = εe^iθ, where z - a represents a vector from point a to point z on Γ with an amplitude of θ. Thus z = a + εe^iθ , 0 θ 2π. Since dz = iεe^iθdθ, 1) becomes

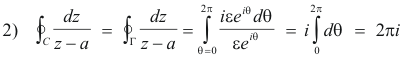
We now prove Part 2.

II Prove: If C be a simple closed curve containing point a in its interior, then

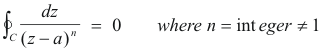
Proof. Again we construct circle Γ as in part I and by reasoning similar to the above we have