Prove. If a function f(z) is analytic inside and on the boundary C of a simply-connected region R, then all its higher order derivatives exist and are analytic in R. For a given interior point a

where C is traversed in the positive (counterclockwise) sense.

Proof. By the definition of a derivative

By Cauchy’s integral formula

and

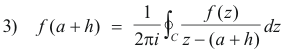
Substituting 2) and 3) into 1) we get

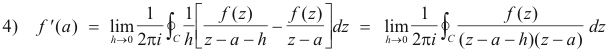
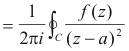
Which proves the theorem for f '(z). Proceeding in the same way we can obtain the formulas

            ..........................................................

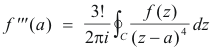
References

  Wylie. Advanced Engineering Mathematics