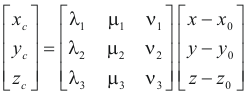
Website owner:  James Miller

            TRANSFORMATION OF COORDINATES

To transform an equation of a surface from an old system of rectangular coordinates (x, y, z) to a new system of rectangular coordinates (x', y', z'), substitute for each old variable in the equation of the surface its expression in terms of the new variables.

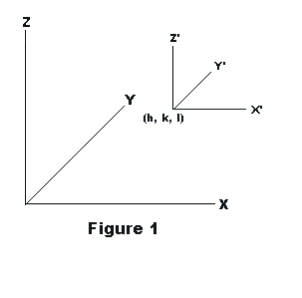
Translation of coordinate system. Let the origin of the new x'-y'-z' system be at point (h, k, l) of the old x-y-z system with the axes of the new system parallel to the corresponding axes of the old system. Then

x = x' + h

y = y' + k

z = z' + l

See Figure 1.                                                   

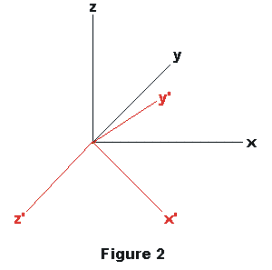
Rotation of the axes about the origin. Let the origin of the new x'-y'-z' system be coincident with the origin of the old system and let λ₁, μ₁, ν₁ be the direction cosines of the x' axis, λ₂, μ₂, ν₂ be the direction cosines of the y' axis, λ₃, μ₃, ν₃ be the direction cosines of the z' axis.

 Then

            x = λ₁x' + λ₂y' + λ₃z'

1)        y = μ₁x' + μ₂y' + μ₃z'

            z = ν₁x' + ν₂y' + ν₃z'

            x' = λ₁x + μ₁y + ν₁z

2)        y' = λ₂x + μ₂y + ν₂z

            z' = λ₃x + μ₃y + ν₃z

We can write these equations in matrix form as

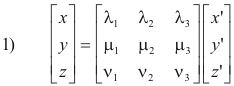
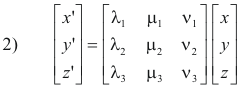
where the matrices are called rotation matrices. Multiplication by a rotation matrix transforms the coordinates of a point from one system to another system.

Note. Equation 1) is best understood in vector terms as a change of basis where 1) is equivalent to

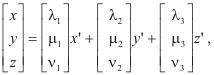
the vectors

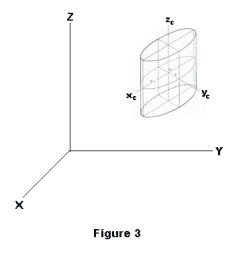
representing orthogonal, unit basis vectors.

Equations relating the coordinates of the original and canonical coordinate systems of a quadric surface. Let x, y and z be the coordinates of a point P with respect to the original X-Y-Z coordinate system and x_c, y_c and z_c be the coordinates of the point with respect to the canonical X_c-Y_c-Z_c coordinate system. See figure 3. Let the origin of the canonical X_c-Y_c-Z_c system be located at (x₀, y₀, z₀) and let λ₁, μ₁, ν₁ be the direction cosines of the x_c axis, λ₂, μ₂, ν₂ be the direction cosines of the y_c axis, λ₃, μ₃, ν₃ be the direction cosines of the z_c axis. Then the relationship between the coordinates x, y, and z and x_c, y_c and z_c is given by the following equations:

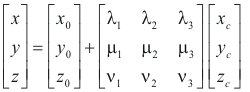
and