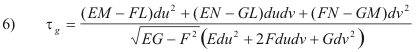Torsion of a geodesic. The torsion of a geodesic passing through point P of a surface in the direction of the unit tangent vector T is given by

where is the unit surface normal at point P and is the position vector at point P, or, equivalently, by

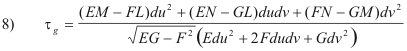
where E, F, G, L, M, N are the first and second fundamental coefficients. 

Derivation. We begin with the Frenet-Serret formula

1)        dn/ds = τ_gB - κT

which relates the geodesic torsion τ_g on the curve at point P to the quantities κ, T, n and B where T, n and B are the unit tangent, principal normal and binormal vectors to the curve at point P. We now take the dot product of both sides of 1) with the vector B

(dn/ds)∙B = (τ_gB - κT)∙B

(dn/ds)∙B = τ_gB∙B - κT∙B

Now B∙B = 1 and T∙B = 0 so

τ_g = (dn/ds)∙B

Now a geodesic C on a surface S has the properties that at each point of C the principal normal coincides with the normal to S. Hence n = N where N is the unit surface normal at P. Letting n = N we have

2)        τ_g = (dN/ds)∙B

Now B = T n = T N. Substituting B = T N into 2) we have

3)        τ_g = (dN/ds)∙(T N)

Now T = where is the position vector of point P on the curve. Substituting into 3) we have

Now = du + dv and dN = N_udu + N_vdv) so

5)        dN N = ( du + dv ) (N_udu + N_vdv)∙N

                        = (N _u N)du² + [N _u N + N _v N ]dudv + (N _v N)dv²

Now setting N = / in 5) and evaluating all products , 4) becomes