Beltrami’s formula for geodesic curvature. Given a curve C: u = u(s), v = v(s) on a surface S: where s is arc length. Beltrami’s formula for the geodesic curvature at point P of the curve is:

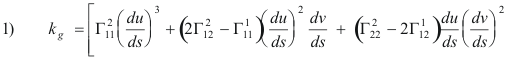
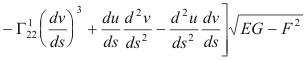
where the Γ_ij^k are the Christoffel symbols of the second kind.

Derivation. We start with the formula of Theorem 3:

If point P on curve C of surface S is represented by the position vector then k_g is given by the following box product

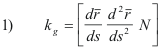
where N is the normal to the surface at P. Now

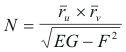
so we can write 1) as

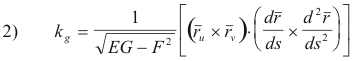
Now

Substituting 3) and 4) into 2) and expanding we get Beltrami’s formula,

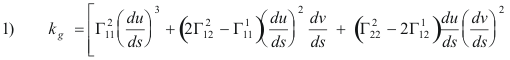
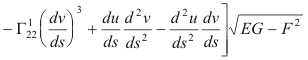
where the Γ_ij^k are the Christoffel symbols of the second kind.