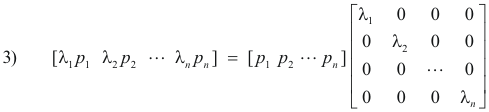
Proof of Theorem 6].

We are given n linearly independent eigenvectors p₁, p₂, ... , p_n of n-square matrix A and the corresponding eigenvalues λ₁, λ₂, ... , λ_n. An eigenvector is a vector X that a matrix A carries into a multiple of itself according to the equation AX = λX where λ is the corresponding eigenvalue. Thus the eigenvectors p₁, p₂, ... , p_n and eigenvalues λ₁, λ₂, ... , λ_n must satisfy the following set of equations:

            Ap₁ = λ₁p₁

1)        Ap₂ = λ₂p₂

            ............

            Ap_n = λ_np_n .

Now system 1) is equivalent to

2)        A[p₁ p₂ ... p_n] = [λ₁p₁ λ₂p₂ ... λ_np_n] .

Why? Because of the following theorem:

______________________________________________

Theorem 1. Suppose that the matrix A carries the vector X₁ into the vector Y₁, the vector X₂ into the vector Y₂ , etc. i.e.

                                    AX₁ = Y₁

                                    AX₂ = Y₂

                                        ......

                                        ......

                                    AX_n = Y_n

Then                           

                           A [ X₁ X₂ .... X_n] = [Y₁ Y₂ ... Y_n]

where [ X₁ X₂ .... X_n] is a matrix whose columns are X₁, X₂, .... , X_n and [Y₁ Y₂ ... Y_n] is a matrix whose columns are Y₁,Y₂, ... ,Y_n .

_____________________________________________________

Furthermore,

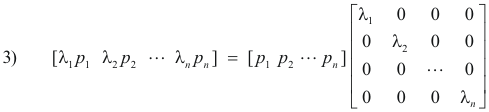
Why? Because of the following theorem:

______________________________________________

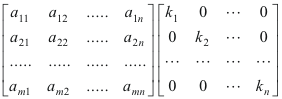
Theorem 2. The effect of post-multiplying a matrix

by a diagonal matrix

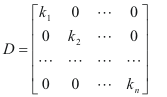
is that of multiplying the i-th column of matrix A by the factor i.e. the successive columns of the original matrix are simply multiplied by successive diagonal elements of the diagonal matrix. Explicitly:

______________________________________________

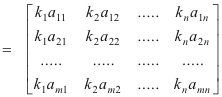
From equations 2) and 3) we get

            AP = PD

or, equivalently,

4)        A = PDP^-1

where we have substituted P for [p₁ p₂ ... p_n] and D for