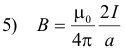
Website owner: James Miller
Prove. The magnetic field intensity B at a perpendicular distance a from the axis of a long straight wire carrying a current I is

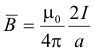
Proof. Let us use the Biot formula
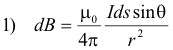
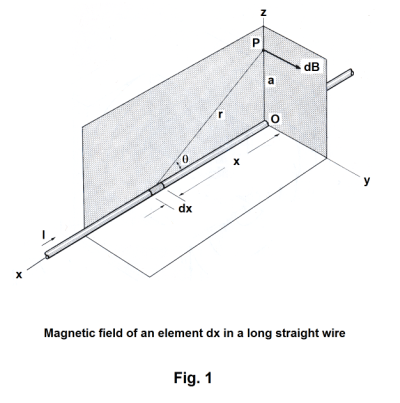
to compute B. We set up an xyz coordinate system as shown in Fig. 1 with the x axis coinciding with the wire and the origin O arbitrarily chosen somewhere on the wire. Let x be the distance from O to a differential element dx, r be the distance from dx to P, and θ be the angle between dx and r. Then formula 1) becomes
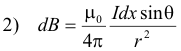
The dB vectors at point P arising from all incremental elements dx on the wire coincide. This means we can do an algebraic sum instead of a vector sum and can use regular integration to sum the dB’s. Integrating, we get
![]()
To facilitate integration, we make a change of variables. From Fig. 1, we see that
r = a csc θ x = a cot θ
Thus
dx = -a csc2θ dθ
Substituting these expressions into 3) gives
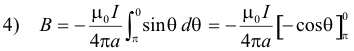
or