Website owner:  James Miller

Prove. The equivalent capacitance C_E of n capacitors C₁, C₂, ... , C_n connected in series is given by 

where C₁, C₂, ... , C_n are the capacitances of the capacitors.

Proof. We will prove it for three capacitors C₁, C₂, and C₃.

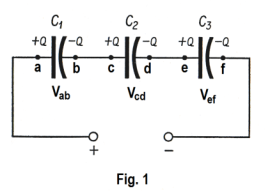
Referring to Fig. 1, if the left plate of capacitor C₁ receives a charge +Q, then an equal negative charge -Q will be induced on the right plate. Now if a negative charge -Q appears on the right plate of C₁, then a positive charge +Q must appear on the left plate of C₂ since the right plate of C₁, the left plate of C₂, and the wire connecting them can be viewed as a single electrical conductor that was originally uncharged and is isolated from the rest of the circuit. Thus each capacitor receives a charge of magnitude Q on each of its plates as shown in the figure. Now

2)      V_af = V_ab + V_cd + V_ef

and, by definition of capacitance,

3)         C₁ = Q / V_ab             C₂ = Q / V_cd              C₃ = Q / V_ef

Substituting 3) into 2) gives

4)        V_af = Q / C₁ + Q / C₂ + Q / C₃

Now an equivalent capacitance C_E for this arrangement is the capacitance of a single capacitor that would become charged with the same charge Q when the potential difference across its terminals is V_af . Consequently,

5)        C_E = Q / V_af

From 4) and 5) we get

6)        Q / C_E = Q / C₁ + Q / C₂ + Q / C₃

which becomes

6)        1 / C_E = 1 / C₁ + 1 / C₂ + 1 / C₃

We note that the energy of the single equivalent capacitor is equal to the sum of the energies of capacitors C₁, C₂, and C₃. The energy of the equivalent is ½ QV_af and the sum of the energies of

capacitors C₁, C₂, and C₃ is ½ QV_ab + ½ QV_cd + ½ QV_ef = ½ QV_af .