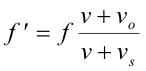
Website owner:  James Miller

Prove. Let f be the emitted frequency, f' be the observed frequency, v be the velocity of sound, v_o be the velocity of the observer and v_s be the velocity of the source where v_o and v_s can be either positive or negative. Let the positive directions of v_o and v_s correspond to that of a vector extending from observer to source. Then                                                                               

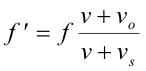
Derivation. In Fig. 1, the observer is at the left and the source is at the right and the positive direction is from left to right. The sound source is at point b at time t = 0 and at point c at time t. The outer circle represents the wave front of the wave emitted at time t = 0. It corresponds to a sphere in three dimensional space and moves outward with a velocity v (The fact that the wave originated at a moving source does not affect its velocity after leaving the source.) The radius ba of this sphere is thus vt. The distance bc equals v_st. Thus

            distance ac = vt + v_st = (v + v_s)t

            distance cd = vt - v_st = (v - v_s)t

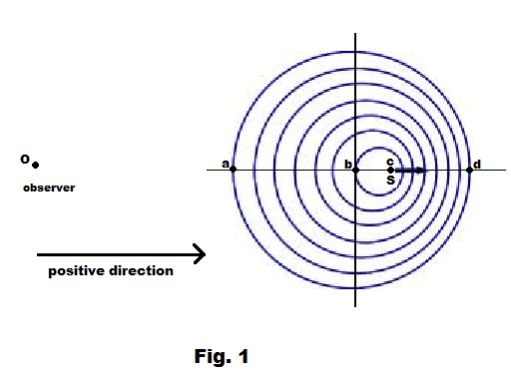
In the time interval from t = 0 to t = t, the number of waves emitted by the source is ft. In front of the source the waves are crowded into the distance cd and behind the source they are spread out over the distance ac. The wavelength in front of the source is thus

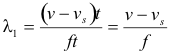
and the wavelength behind the source is

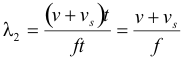
The wave fronts are approaching the observer at an effective speed of v + v_o . The time interval between the time when wave front i passes the observer and when wave front i+1 passes the observer is given by

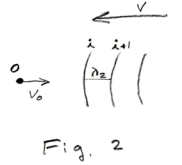
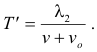
See Fig. 2. The frequency he hears is then

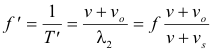
If we consider the case where the observer is stationed to the right of the source, we get the same formula.