Website owner:  James Miller

Prove: During an adiabatic process,

where γ = C_p / C_v .

Proof. In an adiabatic process

            ΔU + W = 0

So

1)        dU + pdV = 0

Now

            dU = nC_Vdt                where n is the number of moles of gas

Substituting into 1) we get,

2)        nC_Vdt + pdV = 0

Since pV = nRT, p = nRT/V. Substituting into 2),

Dividing through by nC_VT,

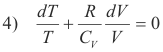
Now

5)        R = C_P - C_V

Dividing 5) by C_V gives

6)        R/C_V = γ - 1

Substituting 6) into 4)

Integrating gives

8)        ln T + (γ - 1)ln V = ln const.

Taking antilogs

or, stated differently,

which is one of the equations we wished to prove. To derive the other we use pV = nRT and substitute T = pV/nR into 9) to get

or

which can be rewritten as