Website owner: James Miller
INTEGRATION BY PARTS
A study of integration is largely a study of methods of transforming various types of integrands into forms in which the fundamental integration formulas can be applied.
Integration by parts. One of the most useful aids to integration is the process known as integration by parts. The formula for the differential of a product
d(uv) = udv + vdu
may be written
udv = d(uv) - vdu .
Integrating both sides, we obtain
![]()
which is the formula for integrating by parts. In order to use this formula we must regard the given integrand as the product of a function u and the differential dv of another function v. There is no general rule that one can give for breaking the integrand into two parts. One usually takes as much of it as he can easily integrate as dv and calls the remainder u. Two rules can be stated, however:
(a) the part selected as dv must be readily integrable.
(b) ∫ v du should not be more complex than ∫ u dv
Example 1. Find
![]()
Solution. We can integrate ex dx, so let us choose u = x and dv = ex dx.
Then du = dx and
![]()
Then our integral becomes, integrating by parts,
![]()
![]()
and this last integral is one of the standard forms. Hence
![]()
Example 2. Find
![]()
Solution. Set u = x2 and dv = sin x dx.
Then du = 2x dx and v = -cos x.
Using the formula
![]()
![]()
Note that this integral is of the same type except that we have x instead of x2 as a multiplier of the trigonometric part. We therefore apply the rule once more to the integral
![]()
Set u = x and dv = cos dx. Then du = dx and v = sin x. Our integral then becomes
![]()
= -x2 cos x + 2x sin x + 2 cos x + C
In some cases it may be possible to use the procedure illustrated by the following example.
Example 3. Find
![]()
Solution. Set u = ex and dv = sin x dx. Then du = exdx and v = -cos x.
![]()
For the last integral set u = ex, dv = cos x dx. Then du = ex and v = sin x. So
![]()
Transposing we have
![]()
or finally
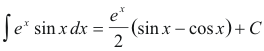
Example 4. Find
![]()
Solution. Set u = x2 and
![]()
Then du = 2xdx and
![]()
by the formula for integrals of functions type un. Then
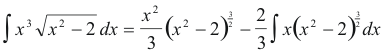
This last integral is again one containing a function of type un so
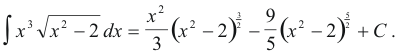
One gains proficiency in this method of integration only by solving many problems. Choosing the parts u and dv is not easy without wide experience.
Method for some special integrals.
● Integrals
![]()
can be evaluated by integration by parts. Set dv = xm dx.
● Integrals of the forms
![]()
can be evaluated by n successive integrations by parts. Set u = xn on the first integration.
Reduction formulas. The labor involved in successive applications of integration by parts to evaluate an integral may be materially reduced by the use of reduction formulas. In general, a reduction formula yields a new integral of the same form as the original but with an exponent increased or reduced. A reduction formula succeeds if ultimately it produces an integral which can be evaluated. Among the reduction formulas are:
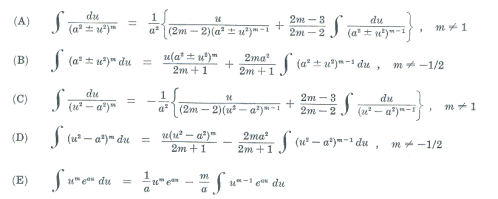
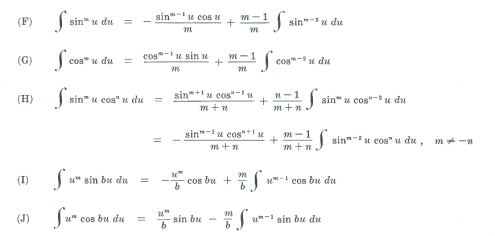
Jesus Christ and His Teachings
Way of enlightenment, wisdom, and understanding
America, a corrupt, depraved, shameless country
On integrity and the lack of it
The test of a person's Christianity is what he is
Ninety five percent of the problems that most people have come from personal foolishness
Liberalism, socialism and the modern welfare state
The desire to harm, a motivation for conduct
On Self-sufficient Country Living, Homesteading
Topically Arranged Proverbs, Precepts, Quotations. Common Sayings. Poor Richard's Almanac.
Theory on the Formation of Character
People are like radio tuners --- they pick out and listen to one wavelength and ignore the rest
Cause of Character Traits --- According to Aristotle
We are what we eat --- living under the discipline of a diet
Avoiding problems and trouble in life
Role of habit in formation of character
Personal attributes of the true Christian
What determines a person's character?
Love of God and love of virtue are closely united
Intellectual disparities among people and the power in good habits
Tools of Satan. Tactics and Tricks used by the Devil.
The Natural Way -- The Unnatural Way
Wisdom, Reason and Virtue are closely related
Knowledge is one thing, wisdom is another
My views on Christianity in America
The most important thing in life is understanding
We are all examples --- for good or for bad
Television --- spiritual poison
The Prime Mover that decides "What We Are"
Where do our outlooks, attitudes and values come from?
Sin is serious business. The punishment for it is real. Hell is real.
Self-imposed discipline and regimentation
Achieving happiness in life --- a matter of the right strategies
Self-control, self-restraint, self-discipline basic to so much in life