Website owner: James Miller
DIFFERENTIABILITY, DIFFERENTIATION RULES AND FORMULAS
Differentiability of a function. A function is said to be differentiable at a point x = x0 if it has a derivative there. A function is said to be differentiable on an interval if it is differentiable at every point of the interval.
In general a function is differentiable on an interval if the function is smooth on that interval, meaning it has no abrupt changes in direction on the interval. If a function has a sharp change in direction at some point the derivative won’t exist at that point. The functions encountered in elementary calculus are in general differentiable, except possibly at certain isolated points on their intervals of definition.
Differentiation rules and formulas. In the following rules and formulas u and v are differentiable functions of x while a and c are constants.
![]()
The derivative of a constant is zero.
![]()
The derivative of a variable with respect to itself is one.
![]()
The derivative of the sum of two functions is equal to the sum of their separate derivatives.
![]()
The derivative of the product of two functions is the first function times the derivative of the second plus the second function times the derivative of the first.
![]()
The derivative of the product of a constant and a function is the constant times the derivative of the function.
![]()
The derivative of the quotient of a function by a constant is the derivative of the function divided by the constant.
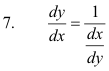
The derivative of y with respect to x is the reciprocal of the derivative of x with respect to y.
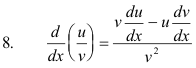
The derivative of the quotient of two functions is the denominator times the derivative of the numerator, minus the numerator times the derivative of the denominator, all divided by the square of the denominator.
9. Let y be a function of u and u be a function of x i.e. y = f(u) and u = g(x). Then
![]()
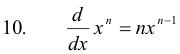
where n is any real number (positive, negative, fractional, etc).
The derivative of the n-th power of x is n times the (n-1)th power of x.
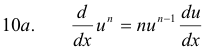
where n is any real number (positive, negative, fractional, etc).
The derivative of the n-th power of a function is n times the (n-1)th power of the function times the derivative of the function.
![]()
where u and v are both variable
Trigonometric functions
![]()
![]()
![]()
![]()
![]()
![]()
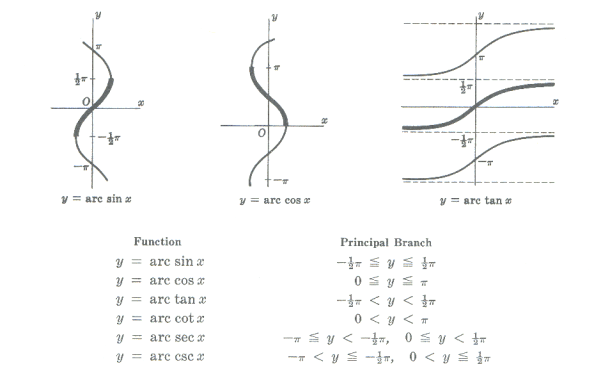
Inverse trigonometric functions
The inverse trigonometric functions are multi-valued. The principal branches are as follows.
![]()
![]()
![]()
![]()
![]()
![]()
Exponential and logarithmic functions
![]()
![]()
![]()
where a is a constant.
![]()
Hyperbolic functions
![]()
![]()
![]()
![]()
![]()
![]()
Inverse hyperbolic functions
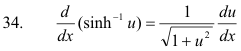
![]()
![]()
![]()
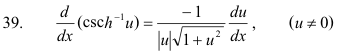
Derivation of formulas
We will now show the derivation of some of the above formulas to illustrate the manner in which they are derived.
Formula 1
![]()
Derivation
Let u and v be differentiable functions of x. If, starting at any fixed value, x increases by an amount Δx, u and v will change by corresponding amounts Δu and Δv, respectively. Then
1) y = u + v
2) y + Δy = u + Δu + v + Δv
Subtracting 1) from 2) gives
3) Δy = Δu + Δv
Dividing by Δx gives
![]()
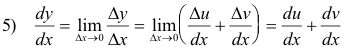
Formula 2
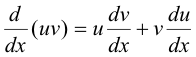
Derivation
Let u and v be differentiable functions of x. If, starting at any fixed value, x increases by an amount Δx, u and v will change by corresponding amounts Δu and Δv, respectively. Then
1) y = uv
2) y + Δy = (u + Δu)(v + Δv) = uv + uΔv + vΔu + ΔuΔv
Subtracting 1) from 2) gives
3) Δy = uΔv + vΔu + ΔuΔv
Dividing by Δx gives
![]()
![]()
Formula 3
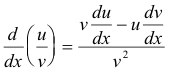
Derivation
Let u and v be differentiable functions of x. If, starting at any fixed value, x increases by an amount Δx, u and v will change by corresponding amounts Δu and Δv, respectively. Then
![]()
![]()
Subtracting 1) from 2) gives
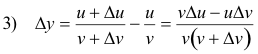
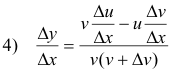
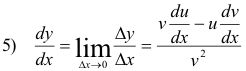
Formula 4
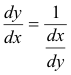
Derivation
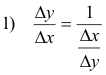
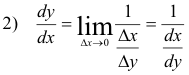
Formula 5
![]()
Derivation
Let u be a differentiable function of x and y a differentiable function of u. If, starting at any fixed value, x increases by an amount Δx, u will change by a corresponding amount Δu and y by an amount Δy, respectively. Then
![]()
Taking limits of both sides as Δx →0
![]()
Formula 6
![]()
Derivation
Let u be a differentiable function of x and
1) y = un .
Then an increment Δx in x produces a change Δu in u and a corresponding change Δy in y giving
2) y + Δy = (u + Δu)n
Expanding (u + Δu)n with the Binomial Theorem gives
![]()
Subtracting 1) from 3) gives
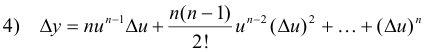
![]()
All terms after the first have the limit zero as Δx →0. Thus taking limits of both sides as Δx →0 gives
![]()
Note. This proof applies only for positive integral values of n. However the formula is valid for all values of n.
Formula 7
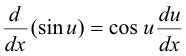
Derivation
Let u be a differentiable function of x. Then
1) y = sin u
2) y + Δy = sin (u + Δu) = sin u cos Δu + cos u sin Δu
Subtracting 1) from 2) gives
3) Δy = sin u (cos Δu - 1) + cos u sin Δu
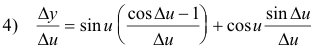
Now
![]()
provide radian measure is used. Why? Two important theorems:
![]()
Thus
![]()
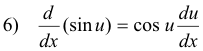
Formula 8
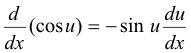
Derivation
To differentiate cosine u we note that
cos u = sin (π/2 - u)
and use the formula for differentiating the sin of a function. Thus
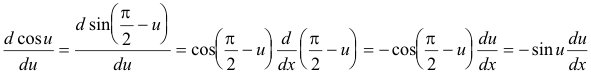
Formula 9
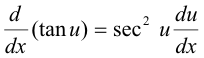
Derivation
The formula for the derivative of tan u can be obtained by writing
tan u = sin u / cos u
and differentiating the quotient.
Jesus Christ and His Teachings
Way of enlightenment, wisdom, and understanding
America, a corrupt, depraved, shameless country
On integrity and the lack of it
The test of a person's Christianity is what he is
Ninety five percent of the problems that most people have come from personal foolishness
Liberalism, socialism and the modern welfare state
The desire to harm, a motivation for conduct
On Self-sufficient Country Living, Homesteading
Topically Arranged Proverbs, Precepts, Quotations. Common Sayings. Poor Richard's Almanac.
Theory on the Formation of Character
People are like radio tuners --- they pick out and listen to one wavelength and ignore the rest
Cause of Character Traits --- According to Aristotle
We are what we eat --- living under the discipline of a diet
Avoiding problems and trouble in life
Role of habit in formation of character
Personal attributes of the true Christian
What determines a person's character?
Love of God and love of virtue are closely united
Intellectual disparities among people and the power in good habits
Tools of Satan. Tactics and Tricks used by the Devil.
The Natural Way -- The Unnatural Way
Wisdom, Reason and Virtue are closely related
Knowledge is one thing, wisdom is another
My views on Christianity in America
The most important thing in life is understanding
We are all examples --- for good or for bad
Television --- spiritual poison
The Prime Mover that decides "What We Are"
Where do our outlooks, attitudes and values come from?
Sin is serious business. The punishment for it is real. Hell is real.
Self-imposed discipline and regimentation
Achieving happiness in life --- a matter of the right strategies
Self-control, self-restraint, self-discipline basic to so much in life